Какой цифрой заканчивается выражение 2015^2015+2016^2016+2017^2017=

С первым числом все понятно: оно заканчивается цифрой 5, поскольку любое число, заканчивающееся пятеркой, в любой степени тоже будет заканчиваться цифрой 5.

Со вторым - аналогично: любое число, заканчивающееся шестеркой, в любой степени тоже будет заканчиваться цифрой 6.

С третьим - немного сложнее. Посмотрим, какой цифрой могут заканчиваться степени числа 2017:

и т.д.. Т.е. последнии цифры степеней числа 2017 чередуются в таком порядке - 7, 9, 3, 1 - и повторяются с интервалом в 4 цифры.

Поскольку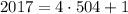 , то последняя цифра числа 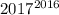- единица. Тогда последняя цифра числа 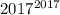- семерка.

Ну а если первое число заканчивается 5, второе - 6, третье - 7, то выражение заканчивается последней цифрой суммы последних цифр всех трех степеней: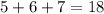 - значит, значение выражения заканчивается цифрой 8.