Каковы координаты вектора, перпендикулярного к вектору АВ {-3; 6}, равного ему по длине?
Другие вопросы по теме Математика
Популярные вопросы
- Спишите,добавляя уточняющие члены к выделенным словам.укажите какое...
2 - Order the letters to make words then fit them into the crossword....
2 - Перевести предложения на язык 1)в каком возрасте у нее было 6 детей?...
3 - 1) 8x+5*(2-3x)=4-6*(10x+3) 2) 3*(x-5)+x=4x-15 3) 2x+5=2*(x+6)...
3 - При каких значениях х выражение 6х-2 принимает положительные значения?...
1 - Найдите и прочитайте сказку до конца,подготовьтесь к читательской...
3 - Есе з укр. мови на тему «що я ціную в людях» до кінця дня 10 ів...
3 - Поставь глаголы в форму 1 го лица единственного числа настоящего...
3 - Действующая сила увеличилась в 2 раза, масса тела увеличилось в...
1 - Практыкаванне 8. часть 2 свирыдзенка в.и...
2
ответ: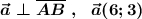 .
.
Скалярное произведение перпендикулярных векторов равно 0 .