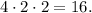1. Математика
  2. Какое наибольшее количество натуральных

Какое наибольшее количество натуральных делителей имеет число āāā ?

Ostap2010 Ostap2010    1   04.08.2022 08:55    1

Ответы
PavlPavl PavlPavl  04.08.2022 08:56

16

Пошаговое объяснение:

\overline {aaa} = 100a + 10a + a = 111a = 3 \cdot 37 \cdot a.

В зависимости от значения a данное число может иметь два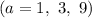 (a = 1,\,\,3,\,\,9) или три 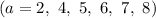(a = 2,\,\,4,\,\,5,\,\,6,\,\,7,\,\,8) простых делителя и далее увеличение количества делителей числа зависит от степени вхождения каждого делителя.

Поэтому среди чисел с двумя делителями наибольшее количество делителей дает цифра 9:

3 \cdot 37 \cdot 9 = {3^3} \cdot {37^1}.

Так как каждый из сомножителей может входить в делитель в любой из степеней, в т. ч. нулевой, количество вариантов для тройки 4, а для тридцати семи — 2, общее количество делителей по правилу произведения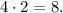 4 \cdot 2 = 8.

Среди чисел с тремя делителями наибольшее количество делителей дает цифра 8:

3 \cdot 37 \cdot 8 = {2^3} \cdot {3^1} \cdot {37^1}.

Аналогично предыдущему случаю, количество делителей равно 4 \cdot 2 \cdot 2 = 16.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Tosya111 Tosya111  15.04.2019 19:40
Машина проехала путь длиной 360 км за 2t часа за сколько часов машина проедет дорогу если будет ехать со скоростью на 5 км больше s - 360 v - ? t - 2t...
maulee502owkszf maulee502owkszf  15.04.2019 19:40
4,2х+5,4(х+0,2)=3,96 4,2х+5,4х+1,08=3,96 9,6х=2,88 просто объясните почему в этом уравнении вдруг появляется число 1,08...
Andreyzem4 Andreyzem4  15.04.2019 19:42
30 используйте все цифры и символы ровно один раз, чтобы записать три верных равенства. а) 1 2 3 4 5 5 6 8 9 9 + × × = = = б) 1 1 3 4 5 5 6 6 7 8 + + × = = =...
maksikus1 maksikus1  15.04.2019 19:42
С, важно: з (с решением)заранее номера: 355 и 356...
dneprovskaya20 dneprovskaya20  15.04.2019 19:43
Впрямоугольном треугольнике один из катетов равен 40 а угол лежащий напротив него равен 45. найдите площадь треугольника...
ангелина618 ангелина618  15.04.2019 19:43
Решыте пример 5a-2x=2a+3x якщо a= -5...
Ren484 Ren484  15.04.2019 19:43
Велосипеде в ехал 1 час 20минут по шоссе. а потом 40 минут по лесной дороге. и проехал всего 28 км .с какой скоростью он ехал по шоссе, если его скорость по лесу на...
diduh2002 diduh2002  15.04.2019 19:43
Учащихся 2 классов поручено расчистить школьный каток длина которого 33м ширина 20 м в одном классе 32 учащихся в другом 28 учащихся сколько квадратных метров кратко...
iququwisjjs iququwisjjs  15.04.2019 19:44
Вкаких случаях a верно выражение -a a , )...
MikasaHasegava MikasaHasegava  15.04.2019 19:44
Вычислите сумму натуральных решений неравенств: 1) × 10; 2) 4 ×; 3) у 13; 4) 14 у.​...

Популярные вопросы