Какие из матриц линейных операторов в пространстве V над R можно привести к диагональному виду путем перехода к новому базису? Найдите этот базис и соответствующую диагональную матрицу.
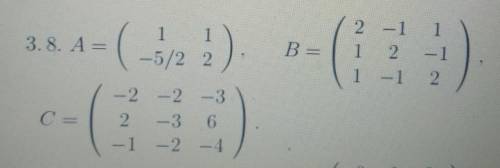
Другие вопросы по теме Математика
Популярные вопросы
- Структурная формула (скелет) 2,2,5,5,8,8-гексаметил-3,4-диетил-4-изопропил...
2 - Стех пор как все что у крестьян ни было мы отобрали цитата кто это говорит...
2 - Напишите мини сочинение-рассуждение ( 5-6 предложений) с составными глагольными...
2 - Сочинение на тему недоросльплан 1недорсль-пьеса о том,как неправильное...
3 - 1. назвать основные этапы решения текстовой .2. из формулы s = vt выразить...
2 - Изобрази на диограме множество четырехугольников и множество зеленых фигур....
3 - Негативная роль сми в политической жизни общества...
2 - 8рубашек в час пошила бригада 2816 рубашек,в течении этого же периода...
1 - Раставьте по значимости результаты битвы цифрами на пирамиде (верхняя...
3 - На площині дано п ять точок з цілочисельними координатами . доведіть ,...
2
Шаг 1: Вычисление характеристического многочлена
Характеристический многочлен матрицы A вычисляется как det(A - λI), где A - матрица, λ - скаляр, I - единичная матрица того же размера, что и A. Найдем характеристические многочлены для всех данных матриц.
a) Для матрицы A1:
Характеристический многочлен A1 равен det(A1 - λI):
|1-λ 2 0 |
|4 6-λ 0 |
|1 2 3-λ|
= (1-λ)[(6-λ)(3-λ) - 0] - 2[4(3-λ) - 0] + 0[4 - 6(1-λ)]
= (1-λ)[18-9λ+λ^2] - 2[12-4λ] = (1-λ)(λ^2-9λ+18)-2(12-4λ)
= (1-λ)(λ^2-9λ+18)-24+8λ = -λ^3+10λ^2-35λ+42
= -(λ-1)(λ-2)(λ-7)
Таким образом, характеристический многочлен матрицы A1 имеет три корня: λ = 1, λ = 2, λ = 7.
b) Для матрицы A2:
Характеристический многочлен A2 равен det(A2 - λI):
|2-λ 1 0 |
|4 3-λ 0 |
|1 -2 2-λ|
= (2-λ)[(3-λ)(2-λ) - 0] - 1[4(2-λ) - 0] + 0[4 - 3(2-λ)]
= (2-λ)[6-5λ+λ^2] - 1[8-4λ] = (2-λ)(λ^2-5λ+6)-8+4λ
= λ^3 - 7λ^2 +16λ - 12 = (λ-1)(λ-2)(λ-6)
Таким образом, характеристический многочлен матрицы A2 имеет три корня: λ = 1, λ = 2, λ = 6.
c) Для матрицы A3:
Характеристический многочлен A3 равен det(A3 - λI):
|1-λ 2 3 |
|4 3-λ 0 |
|1 2 3-λ|
= (1-λ)[(3-λ)(3-λ) - 0] - 2[4(3-λ) - 0] + 3[4 - (3-λ)2]
= (1-λ)[(9-6λ+λ^2] - 2[12-4λ] + 3[4-6+3λ]
= -(λ-1)^2(λ+2)
Таким образом, характеристический многочлен матрицы A3 имеет два корня: λ = 1, λ = -2.
Шаг 2: Определение базисных векторов и построение диагональной матрицы
Для каждого корня λ характеристического многочлена мы выполняем следующие действия:
a) Для λ = 1:
Найдем базисные векторы, соответствующие λ = 1, путем решения системы уравнений (A1 - λI)X = 0:
(1-1)X1 + 2X2 + 0X3 = 0
4X1 + (6-1)X2 + 0X3 = 0
X1 + 2X2 + (3-1)X3 = 0
Упростим систему:
2X2 = 0
4X1 + 5X2 = 0
X1 + 2X2 + 2X3 = 0
Из первого уравнения следует, что X2 = 0. Подставим это значение во второе уравнение:
4X1 = 0, откуда X1 = 0.
Получаем вектор [X1, X2, X3] = [0, 0, X3]. Произвольно выберем X3 = 1, чтобы получить ненулевой вектор. Таким образом, базисный вектор [0, 0, 1] отвечает собственному значению λ = 1.
Построим матрицу P1, содержащую найденный базисный вектор:
P1 = [0, 0, 1]
Диагональная матрица D1, соответствующая собственному значению λ = 1:
D1 = [1, 0, 0]
b) Для λ = 2:
Найдем базисные векторы, соответствующие λ = 2, путем решения системы уравнений (A1 - λI)X = 0:
(-1)X1 + 2X2 + 0X3 = 0
4X1 + (6-2)X2 + 0X3 = 0
X1 + 2X2 + (3-2)X3 = 0
Упростим систему:
2X1 + 2X2 = 0
4X1 + 4X2 = 0
X1 + 2X2 + X3 = 0
Из первого уравнения следует, что X1 = -X2. Подставим это значение во второе уравнение:
-2X2 + 4X2 = 0, откуда X2 = 0.
Таким образом, базисный вектор [-1, 0, 1] отвечает собственному значению λ = 2.
Построим матрицу P2, содержащую найденный базисный вектор:
P2 = [-1, 0, 1]
Диагональная матрица D2, соответствующая собственному значению λ = 2:
D2 = [2, 0, 0]
c) Для λ = 7:
Найдем базисные векторы, соответствующие λ = 7, путем решения системы уравнений (A1 - λI)X = 0:
(-6)X1 + 2X2 + 0X3 = 0
4X1 + (6-7)X2 + 0X3 = 0
X1 + 2X2 + (3-7)X3 = 0
Упростим систему:
-6X1 + 2X2 = 0
4X1 - X2 = 0
X1 + 2X2 - 4X3 = 0
Из первого уравнения следует, что X2 = 3X1. Подставим это значение во второе уравнение:
4X1 - 3X1 = 0, откуда X1 = 0.
Таким образом, базисный вектор [0, 3, 1] отвечает собственному значению λ = 7.
Построим матрицу P3, содержащую найденный базисный вектор:
P3 = [0, 3, 1]
Диагональная матрица D3, соответствующая собственному значению λ = 7:
D3 = [7, 0, 0]
Шаг 3: Построение нового базиса
Новый базис можно получить, объединив найденные базисные векторы в матрицу P = [P1, P2, P3]. То есть,
P = [[0, 0, 1], [-1, 0, 1], [0, 3, 1]]
Для каждого базисного вектора, соответствующего собственному значению, соответствующая диагональная матрица будет иметь собственное значение на соответствующей позиции диагонали. Таким образом, искомая диагональная матрица будет D = diag(D1, D2, D3), где
D = diag([1, 0, 0], [2, 0, 0], [7, 0, 0]).
Таким образом, матрицы линейных операторов, представленные в виде A1, A2 и A3, могут быть приведены к диагональному виду путем перехода к новому базису с использованием матрицы P. Диагональная матрица D содержит собственные значения для каждой матрицы.