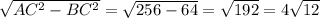Как решить этот то угольник нетпонимаю как ​

1. AC = 12

2. BD = 2

3. DC= 4; AC =16; AB=4 \sqrt{12}

Пошаговое объяснение:

1. DE треугольника DBE находится по теореме Пифагора: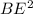 =  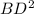 +  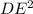, где DE=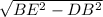

Так как DE = средняя линия треугольника ABC (AD = DB) то AC = 2DE. Отсюда, AC= 12

2. AC находится по той же теореме Пифагора:  AC =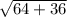=10

BD = медиана треугольника ABC, так как она делит AC на равные отрезки, тогда

BD =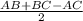 = (6+8-10)/2 =2

3. DC= 4 - показано на рисунке.

Так как угол DBC треугольника BDC равен 30 градусам, то гипотенуза этого треугольника будет равна 8, потому что катет, лежащий против угла в 30 градусов в прямоугольном треугольнике равен половине гипотенузы. Значит BC = 8.

Если угол DBC = 30 градусов, то смежный ему угол DBA= 60 градусов, так как угол ABC = 90 градусов. Теперь рассмотрим прямоугольный треугольник ADB. Если угол DBA = 60 градусов, то угол BAD = 30 градусов. Так как угол BAD =30  граудсов, то BC =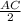 . Получается, что AC = 16. Для нахождения AB применим теорему Пифагора: AB =