Как решать?
тему не понела
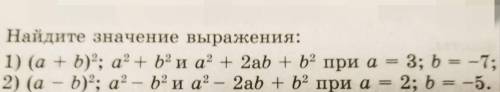
Другие вопросы по теме Математика
Популярные вопросы
- Дано точки А (2; - 1), В (3; 2), C (- 3; 1)....
2 - Визначте межі довжин хвиль звуку яке сприймає наше вухо...
3 - X ^ 0, 3/ x ^ - 1, 8упростить...
1 - У калориметрі знаходиться окріп масою 2 кг. Скільки льоду, взятого при 00C,...
2 - 1. Скласти рівняння реакцій: пропан — 1-фторопропан — пропан-1-ол— пропаналь...
3 - Послідовник нової греко- католицької церкви називається?...
1 - Из приведённых утверждений выберите верные...
3 - Устройство литовского Русского государствапересказ...
3 - вопросы и ЗАДАНИЯ: 1.Почему именно Акбар считается подлинным создателем империи...
3 - История Казахстана Каковы были требования молодежных объединений -шестидесятников»?...
2
В алгебре, да и во всей математике в общем, существуют определенные правила упрощения/сокращения выражений. Они называются формулами сокращенного умножения. Рассмотрим несколько из них:
(a+b)² = a²+2ab+b² - квадрат суммы
(a-b)² = a²-2ab+b² - квадрат разности
a²- b² = (a-b) • (a+b) - разность квадратов
Помимо данных формул есть и другие, связанные с 3 степенью, но для решения данной задачи их знание не понадобиться.
1) Рассмотрим пункт 1. В данном пункте у нас присутствует три выражения, а также нам известно, что a=3, b=-7.
Можно заметить, что выражения (a+b)² и a²+2ab+b² являются формулой квадрата суммы. Поэтому данные выражения равны. Для нахождения их значения достаточно решить хотя бы одно из них. Для удобства, я решу всё.
(a+b)²
(3+(-7))² = (3-7)² = (-4)² = 16
a²+2ab+b²
3²+2•3•(-7)+(-7)² = 9+(-42)+49 = 9-42+49 = 16
a²+b² не является формулой сокращенного умножения, поэтому просто находим значение выражения.
3²+(-7)² = 9+49 = 58
2) Рассмотрим пункт 2. В данном пункте у нас присутствует три выражения, а также нам известно, что a=2, b=-5.
Заметим, что выражение (a-b)² и a²-2ab+b² являются формулой квадрата разности. Поэтому выражения равны. Для нахождения их значения достаточно решить хотя бы одно из них. Я же снова решу всё.
(a-b)²
(2-(-5))² = (2+5)² = 7² = 49
a²-2ab+b²
a²-2ab+b² = 2²-2•2•(-5)+(-5)² = 4-(-20)+25 = 4+20+25 = 49
a²-b² является формулой разности квадратов. Поэтому данное решение можно представить и решить двумя .
a) a²-b²
2²-(-5)² = 4-25 = -21
б) (a-b) • (a+b)
(2-(-5)) • (2+(-5)) = (2+5) • (2-5) = 7•(-3) = -21
ответ будет следующим:
1) 16; 58 и 16
2) 49; -21 и 49