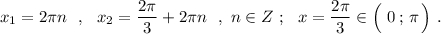, КАК РЕШАЕТСЯ
ОТВЕТ И ОБЪЯСНЕНИЕ
Другие вопросы по теме Математика
Популярные вопросы
- З яким прискоренням з’їжджає візок по похилих рейках, якщо ухил...
2 - (tgx-5)(ctgx+ √3)=0 Математика Решите...
1 - Определите, какое число будет напечатано в результате выполнения...
3 - решить Вычислите ожидаемое соотношение продуктов реакции монохлорирования...
3 - Які великі острови розташовані біля Італії ів...
1 - решить задачу по геометрии (доказательство, куб)...
1 - Ознаки «нової драми» в п’єсі «Ляльковий дім»: 1. П’єса поділена...
2 - Оцени правильность утверждений. А. Близкие по происхождению отряды...
1 - Який інструмент подобається Журдену за його «милозвучність»?...
1 - До 100 г розчину амінооцтової кислоти з масовою часткою розчиненої...
3
Применим формулу косинуса разности .
Из первой серии решений ни одно значение не входит в требуемый интервал .
Из второй серии решений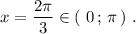
ответ: