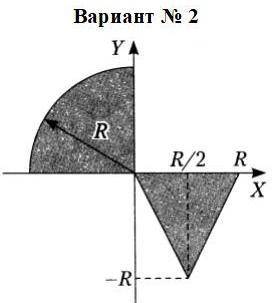
Как проверить попадает ли точка в заштрихованную область?
Другие вопросы по теме Математика
Популярные вопросы
- Эссе Лидеры национально-освободительных восстаний- вдохновители народа...
3 - Выберите правильное утверждение: А) химические реакции происходят в живой...
1 - На каком из рисунков прямые будут параллельны? Поясните свой ответ....
1 - Сколько килограммов нитрата натрия образуется при взаимодействии 500 мл...
3 - Перечислите последствия монгольского нашествия на территории казахстана...
1 - Две проволоки одинаковой длины и поперечного сечения, но из разных материалов,...
3 - От данных глаголов образуй имена существительные. Укажи число и род образованных...
3 - ТЕКСТ ЗАДАНИЯ Объясните понятия:Конфуцианство:Даосизм:Легизм:...
2 - Можете на скриншоте прото точки поставить ...
3 - У геометричній прогресії (bn),b3=20,b4=(-40). Знайти перший член, сьомий...
3
Для x ≤ 0 и y ≥ 0: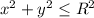
Для x > 0 и y ≤ 0:
Для всех остальных x и y: точка не попадает в заштрихованную область.
Пошаговое объяснение:
Левая заштрихованная область — это четверть круга во второй четверти. Круг задаётся неравенством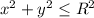 . Ограничения второй четверти: x ≤ 0, y ≥ 0.
. Ограничения второй четверти: x ≤ 0, y ≥ 0.
Правая заштрихованная область — это область выше некоторого модуля. Модуль задаётся уравнением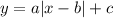 . Так как модуль опущен на R вниз, то c = -R. Так как "вершина" модуля сдвинута на R/2 вправо, то b = R/2. Известно, что точка (0; 0) принадлежит графику модуля. Найдём a:
. Так как модуль опущен на R вниз, то c = -R. Так как "вершина" модуля сдвинута на R/2 вправо, то b = R/2. Известно, что точка (0; 0) принадлежит графику модуля. Найдём a:
Тогда искомое уравнение: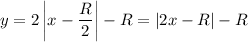
Нужное нам неравенство задаётся так: . Дополнительно также нужно ограничение y ≤ 0.
. Дополнительно также нужно ограничение y ≤ 0.