Как обойти значение 0/0? С каких математических действий? Покажите полное решение
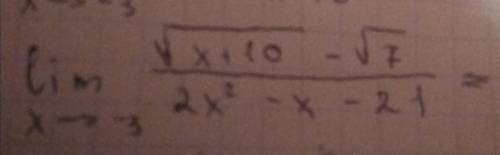
Другие вопросы по теме Математика
Популярные вопросы
- 1. составьте предложение со словами : снизу - ? справа- ? торжественный- ?...
1 - Чудское озеро находится на границе двух государств: россии и столица которой...
1 - Выполните действия: (2/3mn) 3*(-3m) 4...
3 - Масса белого медведя 1000кг, а масса верблюда 600кг. жираф 1200кг, а кролик...
3 - Произведения о хороших поступках автор и название....
2 - Основание прямой призмы - прямоугольный треугольник с гипотенузой 13 см и...
2 - Составить предложение со словами станет,зелёным,красивым...
3 - Наречие - самостоятельная часть речи. чаще всего наречия обозначают признак...
3 - Дана арифметическая прогрессия d: 1,1; a1: -7 s14?...
1 - Какое растение растет только в австралии?...
1
ответ на ваш вопрос "как обойти неопределенность 0/0?" - с взятия производных:
Неопределенность вида раскрывается при правила Лопиталя - если
раскрывается при правила Лопиталя - если 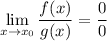 то
то 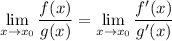
1. Запишемвоспользуемся правилом Лопиталя
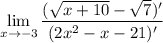
3. Отдельно посчитаю производные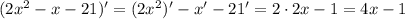
4. Запишем новый предел