1. Математика
  2. Как найти сумму квадратов

Как найти сумму квадратов корней уравнения

Пингвинено25 Пингвинено25    3   13.08.2019 19:16    0

Ответы
smagzamova2006 smagzamova2006  04.10.2020 16:42

ответ: ∑x₁²,x₂²,x₃²=18.

Пошаговое объяснение:

x²*(x-4)-(x-4)=0

(x-4)*(x²-1)=0

(x-4)*(x-1)*(x+1)=0

x₁=4        x₂=1       x₃=-1       ⇒

x₁²+x₂²+x₃²=4²+1²+(-1)²=16+1+1=18.

ПОКАЗАТЬ ОТВЕТЫ
Единорог20001 Единорог20001  04.10.2020 16:42

Ну смотри, это означает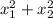 x_{1} ^{2} +x_{2} ^{2}

x^{2} (x-4)-(x-4)=0

(x-4)(x^{2} -1)=0, следовательно

либо первый множитель равен нулю,либо 2

x-4=0 = x_{1} =4

x^{2} -1=0 =x_{2}^{2} =1

x_{2} = 1

x_{3}= -1

прощения,забыл про то,что из квадрата выходит 2 противоположных числа)

Сумма квадратов корней равна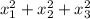 x_{1} ^{2} +x_{2} ^{2}+ x_{3} ^{2} и равна 16+1^{2} + (-1)^2 = 18

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Marina11231 Marina11231  01.06.2020 04:28
2. Обчисли : -1,5 + (-6,5) а.)8 б.)-5 в.)-3 г...
vmyasnikova vmyasnikova  31.05.2020 14:53
Длина стороны большего квадрата равна 1 см. Из этого квадратаотрезали 4 маленьких квадрата, сторона каждого из которых составляет2 стороны большого квадрата. На сколько...
кирилл14373567456 кирилл14373567456  31.05.2020 03:00
Если не трудно Заранее Решите уравнение: sin(5)=12 2. Решите уравнение: cos3=√32 3. Решите уравнение: 22−3cos+1=0 4. Решите уравнение: sin(2)−cos(2)=0 5. Решите уравнение:...
owl2006owl owl2006owl  31.05.2020 14:39
Задати функцію формулою,якщо відомо,що графіком функції є пряма,яка проходить через точки А(1;2) та В(-4;-18)а)y=4x+2b)y=4x-2c)y=-4x+2d)-y=4x-2...
perevalov111222 perevalov111222  31.05.2020 14:15
Зрелый кокос весит полкилограмма. Когда Робинзон расколол кокос пополам и выпил жидкость, он стал весить 62 килограмма. Если бы Робинзон не пил жидкость, а надел одну...
MrGowno MrGowno  31.05.2020 02:04
Конус перетнуто площиною, паралельно основні на відстані 3 см від вершини . Обчисліть площину перерізу , якщо радіус основи дорівнює 12 см ,а висота 9 см...
Умницв Умницв  31.05.2020 14:03
1)Розв язати рівняння а)3,7у=7,77 в)у:5,4=13,5 2)Знайти значення виразу (15,7+14,9):(2,91-1,21) 3)Білий ведмідь важить 720 кг,а маса бурого становить 40%маси білого ведмедя.Обчисліть...
mksmsslvp0b481 mksmsslvp0b481  15.04.2020 14:43
Решите задачи:1. В магазине работает 44 сотрудника. Из них 75% — женщины. Сколькомужчин работает в магазине?2. Катя и Саша собирали грибы. Катя собрала 24 кг грибов, что...
arsigonin arsigonin  15.04.2020 14:43
У девочек - Ани, Иры и Оли было 120 открыток. Больше всего открыток было у Ани. У Иры было в три раза больше чем у Оли. Сколько открыток было у каждой из девочек...
ирмук ирмук  15.04.2020 14:43
У выражение 2k→+4(4j→−4k→)−2(2k→−2j→+2i→) и выбери правильный вариант ответа: −18k→+20j→−4i→ −17k→+21j→−3i→ −17k→+21j→−4i→ −17k→+20j→−4i→...

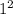Популярные вопросы