КАК ЭТО РЕШИТЬ
Что-то с обратной теоремой Виета
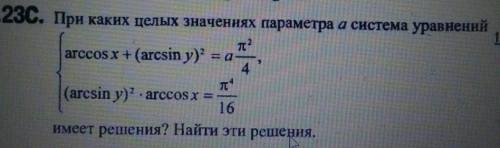
Другие вопросы по теме Математика
Популярные вопросы
- . Спортивні змагання тривали 3 дні. 1 дня взяли участь 32% всіх учасників—...
2 - Баана бааsuauonam? Nonnen ongenennt ma2. Прочитай вис, клинаеш,нии?с другими...
2 - 《Нағыз әже қайда?》әңгімесі Білу:1.Әңгіме кейіпкерлері туралы не білдіңдер?2.Балалары...
1 - Написати про кожну природну зону Євразії. Арктичні пустелі Тундра Лісотундра...
2 - как найти скорость катера против течения если известна скорость течения и...
2 - 5-тапсырма. Нүкте қойылатын орындар берілген. Соларға мысал ойли табыңдар.Баскы...
1 - Написати характеристику образів князя та дракона Грицька...
2 - Камень и дорога допиши пропущенные пункты текста...
2 - Задания Прочитайте отрывок из сказки А.Н. Островского «Снегурочка» Весна-Красна...
1 - 1. Как делятся цвета по их воздействию на человека? а) основные; б) теплые...
1
a=2
Пошаговое объяснение:
1) Из определения функций 0≤arccosx≤π, -π/2≤arcsiny≤π/2
0≤arcsin²y≤π²/4
a·π²/4=arccosx+arcsin²y≤π+π²/4
a·π²/4≤π+π²/4
a≤4/π+1<2+1=3⇒a≤2, так как по условию a∈Z
a·π²/4=arccosx+arcsin²y≥0+0=0
a·π²/4≥0⇒a≥0
0≤a≤2
Пусть arccosx=t₁, arcsin²y=t₂, t₁∈[-π/2; π/2], t₂∈[0; π]
Тогда по обратной теореме Виета числа t₁, t₂ являются корнями уравнения
t²-(t₁+t₂)t+t₁t₂=0
t²-a·t·π²/4+π⁴/16=0
Которое имеет действительные корни при
0≤D=(a·π²/4)²-4·π⁴/16=a²π⁴/16-π⁴/4
a²π⁴/16-π⁴/4≥0
π⁴/16·(a²-4)≥0
a²-4≥0
a∈(-∞; -2]∪[2; +∞)
Учитывая найденное выше неравенство 0≤a≤2 и a∈Z получим a=2
Остается только проверить, что a=2 удовлетворяет данному вопросу.
D=a²π⁴/16-π⁴/4=4·π⁴/16-π⁴/4=π⁴/4-π⁴/4=0⇒t₁=t₂=π²/4
arccosx=arcsin²y=π²/4
arcsin²y=π²/4
arcsiny=±π/2
y=±1
arccosx=π²/4=π·π/4<π·1=π⇒0<arccosx<π
x=cos(π²/4)≈-0,7812