Как доказать,что площадь прямоугольника равна произведению длин его смежных сторон.
Другие вопросы по теме Математика
Популярные вопросы
- Придумать 10 слов чтоб были в родительном и винительном падеже....
3 - Выполни действия 29·9 18·15 927: 3 616: 11 300: 150 870: 435 125·5 230·4 нужно!...
2 - Чем человек отличается от животного ? не большой рассказ....
1 - 1. число р.п.е в ni 2.определить n-? v-? oз грамм,1,8 грамм 3.указать класс...
3 - Рабочие должны изготовить 840 деталей первый изготовил в час 60 деталей а...
3 - Впервый день утром на зарядке в летней образовательной школе сибирского федерального...
3 - Самолёт находится на расстоянии 45 км от радиолокатора вычислите время за...
2 - Составить чайнворд орган 5 вопросов...
2 - Раздели карточки с числами на 3 множества.,1,300,5,6,14,12,400,78,39,200,33,35,100,3,500,2,7,9....
2 - Напишите уравнение окружности если a(7; -10)-ее центр,а радиус равен 5 см...
3
Построим квадрат со сторонами, равными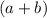 . Поскольку площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна
. Поскольку площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна 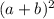 , т.е. как формула сокращённого умножения - квадрат суммы.
, т.е. как формула сокращённого умножения - квадрат суммы.
По свойству, если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Из этого следует, что:
Из этой записи получаем: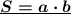 .
.
Что и требовалось доказать (ч.т.д.)ответ: Теорема доказана ☑.