Известно что частное двух чисел на 51 меньше делителя и на 671 меньше делимого. найдите чему равно частное. ​

Обозначим частное за . Тогда из условия можно сделать вывод, что делитель равен 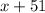, а делимое равно .

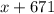Так как {делимое} / {делитель} = {частное}, то:

И решаем данное уравнение (помня, что ):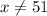

Квадратное уравнение можно решить множеством

Например, можно применить теорему Виета (она гласит, что в данном случае и 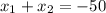). Так как 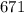делится нацело на не такое уж большое количество чисел, то можно сделать вывод, что 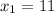и .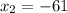

Можно и решить дискриминантом (хотя это в данном случае несколько сложнее в плане вычислений):

Таким образом, это могло быть одно из чисел и :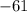

Задача решена!