Известно, что 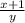
=
=
- целое число. какое наибольшее значение может принимать сумма x+y+z НУЖЕН ОТВЕТ
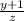
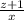
Другие вопросы по теме Математика
Популярные вопросы
- Визначте масу розчину,якщо до 17гр.цукру добавили70гр.води.Виконати...
3 - Запишите уравнения реакций взаимодействия муравьиной кислоты с веществами:...
3 - Подготовьте 5 аргументов из разных областей искусства (архитектура,...
3 - She has never been toAppalachian mountains. It’s dangerous to crossSahara...
2 - Дан фрагмент программы: x:= 83; write ( ответ: , х: 2, км/ч ); На...
2 - Розрахувати при якому навантаженні (кН) повинна зруйнуватись бетонна...
2 - Otliciya mejdu YUJNOY I SEVERNOY KOREEY(LUBLU K-POP)...
2 - Скиньте ответы по английскому страница 104, 8 класс ОТВЕТЫ НЕ ФОТО,...
3 - Стійкість екосистем що проявляється в здатності швидко відновлюється...
2 - В каком из предложений 7- 11 использованы антонимы Напишите номер...
2
По-детски:
Найдем наибольшее значение параметра а, при котором система
{ x+y+z=a,
{ 3x² + 2y² + z =1
имеет решение.
Выразим z из первого уравнения : z=a-x-y и подставим во второе, получим:
3x² + 2y² + a - x - y - 1 = 0.
Выделим полные квадраты:
3(x-1/6)² + 2(y-1/4)² + a - 29/24 = 0
3(x-1/6)² + 2(y-1/4)² = - a + 29/24
Уравнение имеет решение, если - a + 29/24 ≥ 0, т. е. a ≤ 29/24.
Наибольшее значение а (а значит и x+y+z), равноe 29/24, достигается при х=1/6, у=1/4, z=19/24.
ответ: 29/24