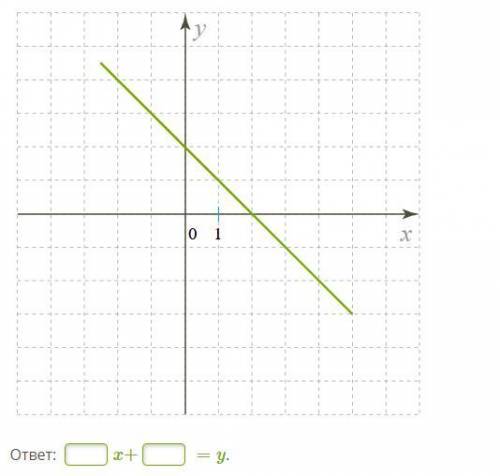
Изучи рисунок и составь к нему формулу для этого графика функции

-x+2=y

Вот как

Добро пожаловать в нашу школу! Рад, что ты интересуешься графиком функции. Давай разберемся с этим вместе.

На данном рисунке мы видим график функции, который может быть представлен в виде прямой линии. Чтобы составить формулу для этого графика функции, нам понадобится информация о координатах двух точек на этой линии.

Для этого выберем две точки, чтобы провести прямую линию. Нам кажется, что на данном графике хорошо видны две такие точки: (0, 3) и (8, 9).

Теперь давайте используем эти две точки и знакомые нам формулы, чтобы найти уравнение прямой, проходящей через них.

Формула для уравнения прямой в общем виде имеет вид y = mx + b, где m - коэффициент наклона прямой, а b - точка пересечения прямой с осью ординат (ось y).

Чтобы найти коэффициент наклона m, мы можем использовать следующую формулу:

m = (y2 - y1) / (x2 - x1),

где (x1, y1) и (x2, y2) - координаты двух точек на графике.

Подставляя в эту формулу координаты выбранных точек (0, 3) и (8, 9), получаем:

m = (9 - 3) / (8 - 0) = 6 / 8 = 3 / 4.

Таким образом, коэффициент наклона прямой равен 3/4.

Далее, чтобы найти точку пересечения с осью ординат (b), мы можем использовать одну из координат точек. Например, мы можем использовать точку (0, 3). Подставляем ее координаты в уравнение прямой:

3 = (3/4)(0) + b.

При умножении 3/4 на 0 получаем 0, поэтому уравнение упрощается:

3 = b.

Таким образом, b равно 3.

Итак, у нас есть значение коэффициента наклона m (3/4) и точка пересечения с осью ординат b (3).

Составив формулу функции на основе этих результатов, получаем:

y = (3/4)x + 3.

Теперь у нас есть полная формула для данного графика функции.

Надеюсь, это объяснение и решение понятны для тебя. Если у тебя возникнут еще вопросы, не стесняйся задавать их! Я готов ответить на все, что тебя интересует.