Из всех прямоугольных параллелепипедов, имеющих данную диагональ, найти тот,объём которого наибольший. Заранее за правильный и верный ответ.

Ответы

Semfore 13.07.2021 19:36

Вообще говоря, эту задачу можно решать с метода множителей Лагранжа, но я постараюсь обойтись без них. Задача максимизировать произведение abc трех положительных чисел при условии постоянства суммы a²+b²+c² их квадратов. Понятно. что вместо произведения чисел можно рассмотреть произведение их квадратов, а обозначив их буквами x, y, z соответственно, получаем более симпатичную формулировку: максимизировать произведение xyz положительных чисел при условии x+y+z=K (K - некоторое положительное число).

$z=K-x-y;\ f(x,y)=xy(K-x-y)=Kxy-x^2y-y^2x.$

$f'_x=Ky-2xy-y^2;\ f'_y=Kx-x^2-2xy.$

Как всегда в таких задачах, ищем точки, в которых обе частные производные равны нулю (иными словами, точки, в которых первый дифференциал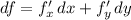 $df=f'_x\, dx+f'_y\, dy$ равен нулю):

$\left \{ {{Ky-2xy-y^2=0} \atop {Kx-x^2-2xy=0}} \right.;\ \left \{ {{K-2x-y=0} \atop {K-x-2y=0}} \right.; \left \{ {{x=K/3} \atop {y=K/3}} \right. .$ Сокращение на x и y оправдано их положительностью. (Кстати, если даже попробовать представить себе параллелепипед с нулевой стороной, шансов у такого вырожденца иметь наибольший объем нет никаких.) Далее теория советует исследовать второй дифференциал $d^2f=f''_{xx}(dx)^2+2f''_{xy}\, dx\, dy+f''_{yy}(dy)^2$ в найденных критических точках на положительную или отрицательную определенность с критерия Сильвестра. Давайте последуем этим советам.

$f''_{xx}=-2y;\, f''_{xx}(\frac{K}{3};\frac{K}{3})=-\frac{2K}{3}; \, f''_{xy}=K-2x-2y;\, f''_{xy}(\frac{K}{3};\frac{K}{3})= -\frac{K}{3};$

$f''_{yy}=-2x;\, f''_{yy}(\frac{K}{3};\frac{K}{3})=-\frac{2K}{3}.$

Видим, что угловой минор первого порядка -2K/3<0; угловой минор второго порядка K²/3>0. Значит, второй дифференциал отрицательно определен, а это в условиях равенства нулю дифференциала первого порядка означает наличие точки максимума.

Итак, доказано, что наибольший объем среди параллелепипедов с фиксированной диагональю имеет куб.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика