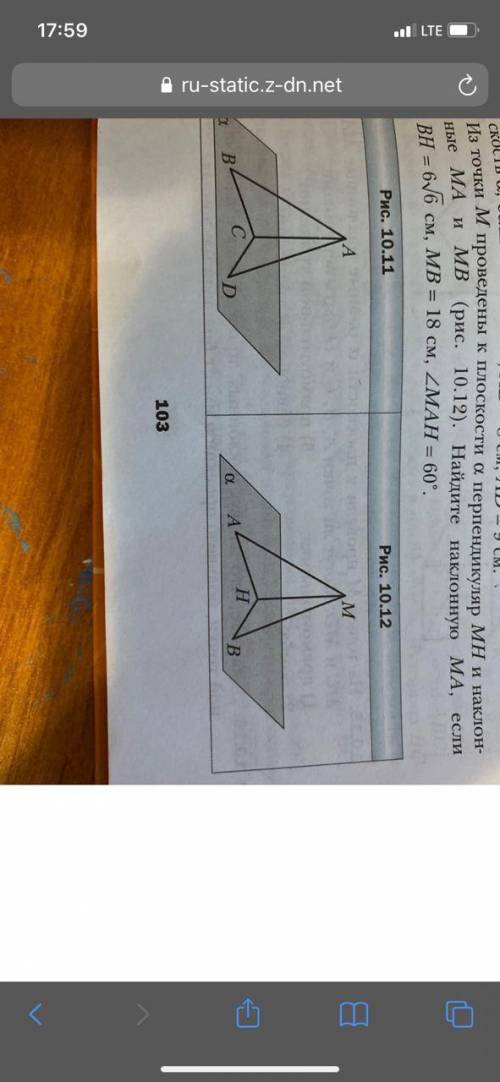
Из точки м проведены к плоскости альфа перпендикуляр mh и наклонные ma mb (рис. 10.12): найдите наклонную ма, если bh = 6 корень из 6, mb = 18 см, угол mah = 60 градусов Решени а не ответ
Другие вопросы по теме Математика
Популярные вопросы
- Подготовьте сообщение о том ,как проводится разработка новых видов и типов...
1 - Почему владимир велел выгнать троекурова? описать сцену....
1 - Аи в - концы отрезка , m - середина. найдите координаты а, если в(4; 7) м...
1 - Найти неизвестный член пропорции 5 ÷7=х ÷120...
3 - 1.какие чувства испытывает владимир дубровский в кстеневской роще? 2.как видут...
2 - 3215 72 12 16 32 1000=3943. расставьте знаки и скобки, чтобы получилось верное...
1 - Какой частью речи выражены обращения?...
1 - Lorry, pig, pen bell, wind, troll, doll, milk, belt, fox, nest, bed, six,...
1 - девочка на шаре -так называеться и знаменитоя картина испанского художника...
1 - Путь из города а в город б поезд за 3 часа проходя каждый час по 45 км ему...
3
Для начала, обратимся к треугольнику MAH. У нас есть известные стороны MA и MH, а также угол MAH, равный 60 градусов. Нам нужно найти длину стороны MA.
Используя теорему косинусов, мы можем записать следующее уравнение:
MA^2 = MH^2 + AH^2 - 2 * MH * AH * cos(MAH)
Здесь MA^2 обозначает квадрат длины стороны MA, MH^2 обозначает квадрат длины стороны MH, AH^2 обозначает квадрат длины стороны AH (которую мы и хотим найти), а cos(MAH) - косинус угла MAH.
Теперь вспомним, что треугольник AHB является прямоугольным, и поэтому у нас есть следующее уравнение:
BH^2 = AH^2 + AB^2
Мы знаем длину стороны BH (она равна 6 корень из 6), хотим найти длину стороны AH, и также знаем длину стороны AB (она равна 18 см).
Теперь мы можем решить эти два уравнения для нахождения длины стороны AH и стороны MA.
Из уравнения BH^2 = AH^2 + AB^2 мы можем выразить AH^2:
AH^2 = BH^2 - AB^2
AH^2 = (6√6)^2 - (18)^2
AH^2 = 36 * 6 - 324
AH^2 = 216 - 324
AH^2 = -108
Поскольку AH^2 получается отрицательным числом, это означает, что треугольник AMA не существует на плоскости альфа. Возможно, в условии была допущена ошибка или опечатка.
Поэтому мы не можем найти длину стороны AH и, соответственно, сторону MA. Ответ на этот вопрос не может быть найден с использованием предоставленных данных.