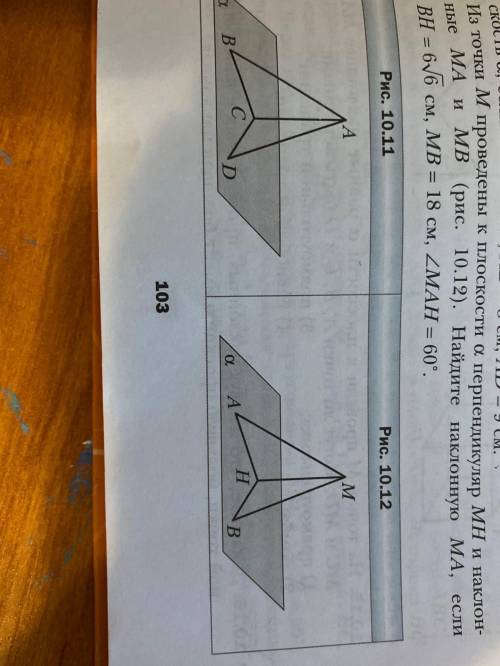
из точки м проведены к плоскости альфа перпендикуляр mh и наклонные ma mb (рис. 10.12): найдите наклонную ма, если bh = 6 корень из 6, mb = 18 см, угол mah = 60 градусов
Другие вопросы по теме Математика
Популярные вопросы
- Что означает? ex 14 - 15 p.g ex 11p 22 -...
1 - Решить . на одном складе было 2200 т. угля а на втором 2800 т. когда со...
3 - Составе эмпирические формулы: alcl3, c2h4...
3 - Найди местоимение в отрывках и укажи лицо и число.! как будильник зазвонит,...
2 - Надо определите знак числа h зная что график функции y=h/x расположен:...
1 - Нужен перевод! shakespeare s literary work is usually divided into three...
2 - Постройте график уравнения |y-1|=x-1...
3 - Уравнение окружности проходящей через точки a (5; 0) .b(1; 4).если центр...
1 - (: нужно пояснить четверостишие державина памятник : …первый я дерзнул...
2 - Паскаль построить программу. циклический алгоритм. a (a-1)(a-2)(a--n)...
2
0 отчёт лшоолдлшщшггвоаочосгчнян
Итак, нам нужно найти длину наклонной ма. Обозначим эту длину как x.
Сначала найдем длину отрезка mh, используя теорему Пифагора в прямоугольном треугольнике mbh:
mh^2 = mb^2 - bh^2
mh^2 = (18 см)^2 - (6√6)^2
mh^2 = 324 см^2 - 216 см^2
mh^2 = 108 см^2
mh = √108 см
mh = 6√3 см
Теперь мы можем использовать теорему Пифагора в прямоугольном треугольнике mah:
ma^2 = mh^2 + ah^2
ma^2 = (6√3 см)^2 + (x)^2
ma^2 = 108 см^2 + x^2
Также нам дано, что угол mah равен 60 градусов. Мы можем использовать тригонометрическую функцию синус для нахождения отношения высоты ah к гипотенузе ma:
sin(60 градусов) = ah / ma
√3 / 2 = ah / ma
ah = (√3 / 2) * ma
Теперь мы можем подставить выражение для ah в уравнение для ma:
ma^2 = 108 см^2 + x^2
(√3 / 2) * ma = ah
ma^2 = 108 см^2 + (√3 / 2)^2 * ma^2
ma^2 = 108 см^2 + (3 / 4) * ma^2
ma^2 - (3 / 4) * ma^2 = 108 см^2
(1 - (3 / 4)) * ma^2 = 108 см^2
(1 / 4) * ma^2 = 108 см^2
ma^2 = (108 см^2) / (1 / 4)
ma^2 = 4 * 108 см^2
ma^2 = 432 см^2
ma = √432 см
ma = 6√12 см
Итак, длина наклонной ma равна 6√12 см.