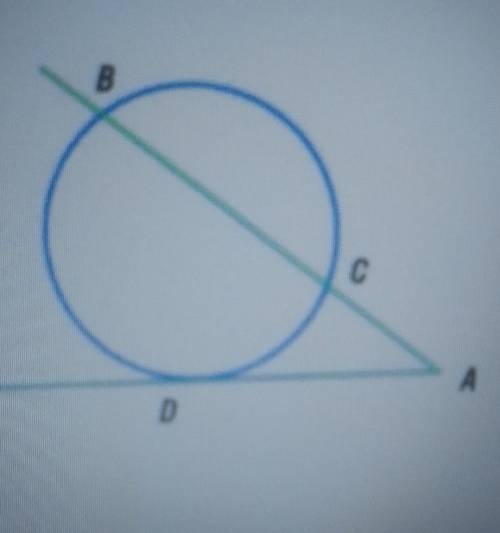
Из точки А проведены секущая AB = 16 и касательная AD к окружности. Найди AD, если известно, что АС на 3 меньше, чем AD, а искомая
касательная AD больше 5.
Другие вопросы по теме Математика
Популярные вопросы
- Вставьте пропущенные буквы, расставьте знаки препинания, раскройте...
1 - Сказка Аня в Стране чудес набоков во Как удалось всем промокшим...
2 - надо. Экспонат № Как повели себя дети по отношению к Анне Федотовне?...
2 - Берілген сөздерден өлең жолдарынқұрастырып айт.ЖасылКентүктіКӨПКакКілемнұрынКілемойнаймынжайлауКүнніңнулемКілемдеайдыңдепсәулесінҚазағымныңмахаббатыКӨПаппақҚЫЗЫЛбілем...
1 - В парке высадили 160 деревьев .Среди них 48 лип. Сколько процентов...
3 - GRAMMAR Tick () A, B, or C to complete the sentences. Example:...
2 - Сумму натурального числа и дроби 8+ смешанным числом...
1 - разложи на множители 2х+6х^2+3х ...
1 - Одну из глав поэмы ,, За далью-Даль ,, охарактеризуйте самостоятельно...
1 - по Истории!! ВНЕШНЯЯ ПОЛИТИКА РОССИ XVII Веке...
2
У нас дана окружность с центром в точке O и точка A находится вне окружности. Проведена секущая AB, где AB = 16, и касательная AD к окружности. Нам нужно найти значение AD.
Чтобы решить эту задачу, давайте воспользуемся теоремой о касательных и хордах: "Если из точки вне окружности проведена касательная и секущая, то произведение отрезков, образованных секущей, будет равно квадрату отрезка, образованного касательной."
Обозначим точку пересечения секущей и касательной как C. По условию задачи, мы знаем, что АС на 3 меньше, чем AD. Значит, AC = AD - 3.
Также условие говорит, что касательная AD больше 5. Значит, AD > 5.
Мы знаем, что произведение отрезков, образованных секущей, будет равно квадрату отрезка, образованного касательной. Мы можем записать это как AB * AC = AD^2.
Подставим известные значения: 16 * (AD - 3) = AD^2.
Раскроем скобки: 16AD - 48 = AD^2.
Перенесем все в правую часть уравнения: AD^2 - 16AD + 48 = 0.
Обратите внимание, что это квадратное уравнение. Мы можем попытаться решить его путем факторизации.
Факторизуем уравнение: (AD - 12)(AD - 4) = 0.
Из этого уравнения получаем два возможных значения для AD: AD = 12 и AD = 4.
Но мы знаем, что AD должна быть больше 5. Поэтому отбросим AD = 4 и оставим AD = 12.
Таким образом, мы получили, что значение AD равно 12.
Для проверки, мы можем подставить это значение в уравнение AB * AC = AD^2: 16 * (12 - 3) = 12^2, 16 * 9 = 144, 144 = 144.
Ответ: AD = 12.
Надеюсь, что я подробно разъяснил вам решение этой задачи. Если у вас остались вопросы или вам нужно что-то еще, пожалуйста, дайте мне знать!