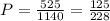Из партии, состоящей из 20 радиоприемников, для проверки произвольно отбирают три приемника. Партия содержит 5 неисправных приемников. Какова вероятность того, что в число отобранных войдут;
а) только исправные приемники;
б) только неисправные приемники;
в) один неисправный и два исправных приемника

а) 191/228

б) 1/114

в) 125/228

Пошаговое объяснение:

Число возможных элементарных исходов для выборки 3 из 20 приемников вычисляем по формуле:

С³₂₀ =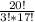 = = 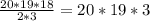1140 (Это общее количество всех возможных комбинаций, когда из 20 приемников выбрали 3)

а) Число "нужных" комбинаций, когда выбрали 3 исправных приемника из 15 исправных:

С³₁₅=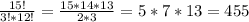

Значит вероятность а) :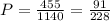 (отношение нужных комбинаций ко всем возможным)

б) Число "нужных" комбинаций, когда выбрали 3 неисправных приемника из 5 неисправных:

С³₅=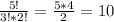

Значит вероятность б) :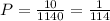

в) Число "нужных" комбинаций, когда выбрали 1 неисправный из 5 неисправных и 2 исправных приемника из 15 исправных равна произведению:

С¹₅ * С²₁₅ =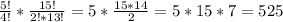

Значит вероятность в) :