Из некоторого пункта выехали одновременно два велосипе. диста, один из которых отправился на запад, а другой на север. Через 4 ч оказалось, что расстояние между ними равно 80 км, при чем первый велосипедист проехал на 12 км меньше второго. С ка Кой скоростью ехал каждый велосипедист? Обозначив через х км/ч скорость первого велосипедиста, а км/ч скорость второго велосипедиста, составили системы уравнений. Какая из них верная?
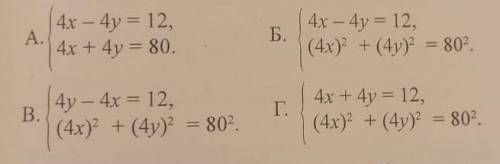
Другие вопросы по теме Математика
Популярные вопросы
- Тема: Двумерные массивы в С/C++ Mассив вывести на экран в виде таблицы...
1 - ВЫПИСАТЬ СУЩЕСТВИТЕЛЬНЫЕ,ГЛАГОЛWhen we make tea and coffee we use energy:...
2 - Мощность, потребляемая из сети электрокамином, равна 0,98 кВт, а сила...
3 - 150см в М2 150см это рост, нужно чтобы был в метрах квадратных определить...
1 - 2-тапсырма. Төменде берілген әр сөйлемді өз сөзіңізбен қайта жазыңыз....
3 - ! ответ должен получиться V=0,995 с...
2 - Краткий конспект Империя в которой никогда не заходило солнце...
3 - 1санька знехотя, сердито й помалу знову лізе на лежанку 2І сльози вже...
2 - ответить на вопросы ~Лучше или хуже демократия других форм правления?~Что...
2 - Указать число, падеж, род, у слова прилагательного большую...
2
Мы знаем, что оба велосипедиста выехали одновременно из одного пункта. Один из них ехал на запад, а другой на север. Из условия задачи видно, что через 4 часа расстояние между ними составляло 80 км.
Пусть скорость первого велосипедиста будет обозначена как V1, а скорость второго велосипедиста - как V2. Также, нам дано, что первый велосипедист проехал на 12 км меньше, чем второй.
Мы можем использовать следующие формулы:
1. Для расчета пути S, пройденного велосипедистом, используем формулу S = V * t, где V - скорость, t - время.
2. Для расчета расстояния между велосипедистами используем теорему Пифагора для прямоугольного треугольника. В нашем случае, одна сторона треугольника будет равна расстоянию, пройденному первым велосипедистом (S1 = V1 * t = (V1 * 4)), вторая сторона будет равна расстоянию, пройденному вторым велосипедистом (S2 = V2 * t = (V2 * 4)), а третья сторона будет равна расстоянию между велосипедистами (80 км).
Исходя из этой информации, мы можем составить следующую систему уравнений:
(V1 * 4)^2 + (V2 * 4)^2 = 80^2
V1 * 4 = V2 * 4 - 12
Теперь решим эту систему уравнений.
Раскроем скобки в первом уравнении и получим:
16V1^2 + 16V2^2 - 192V2 + 144 = 6400
Перенесем все значения влево и приведем уравнение к виду:
16V1^2 + 16V2^2 - 192V2 - 6256 = 0
Также заменим значение V1 из второго уравнения в первое:
(4V2 - 12)^2 + (V2 * 4)^2 = 6400
16V2^2 - 96V2 + 144 + 16V2^2 = 6400
32V2^2 - 96V2 - 6256 = 0
Теперь мы имеем квадратное уравнение, которое можно решить с помощью дискриминанта.
Дискриминант D = b^2 - 4ac
D = (-96)^2 - 4 * 32 * (-6256)
D = 9216 + 200192
D = 209408
Так как D > 0, у нас есть два корня. Решим уравнение:
V2 = (-b + √D) / 2a
V2 = (-(-96) + √209408) / 2 * 32
V2 = (96 + √209408) / 64
V2 = (96 + 458) / 64
V2 = 554 / 64
V2 ≈ 8.65625 км/ч
Теперь найдем V1, подставив найденное значение V2 во второе уравнение:
V1 = (V2 * 4) - 12
V1 = (8.65625 * 4) - 12
V1 = 34.625 - 12
V1 ≈ 22.625 км/ч
Таким образом, первый велосипедист ехал со скоростью около 22.625 км/ч, а второй велосипедист ехал со скоростью около 8.65625 км/ч.
Ответ: Первый велосипедист ехал со скоростью около 22.625 км/ч, а второй велосипедист ехал со скоростью около 8.65625 км/ч.