Из круглого листа вырезать такой сектор, чтобы, свернув его, получить воронку наибольшей вместимости
Другие вопросы по теме Математика
Популярные вопросы
- 10. автобус массой 15 т трогается с места и движется с ускорением 0,7 м/с^2....
3 - 8. масса земли больше массы луны в 81 раз. земля притягивает луну с силой f1.с...
2 - )1.выведите электронно-точечные формулы молекул и ионов. 2.определите тип гибридизации....
2 - Вкаком предложении оба выделенных слова пишутся слитно? 1)мы то(же) решили...
2 - Гипотенуза прямоугольного треугольника равна 15 см, а один из катетов на 3...
1 - Решите уравнение: а) 7,3 в квадрате + m : 2,86=60 b) 45,94+(f-453,12) * 125=...
2 - Разобрать слово в аллее под цифрой 3 и составить предложение со словосочетанием...
1 - Какой отказ от первого приема наркотика является самым убедительным?...
2 - При каких значениях m верно m² m ?...
1 - Решить ! какие из урверждений не являются верными? 1) если два угла одного...
1
Пусть - длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.
- длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.
Пусть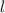 - радиус круглого листа и одновременно образующая конуса (воронки).
- радиус круглого листа и одновременно образующая конуса (воронки).
Тогда радианная мера дуги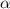 , ограничивающей искомый сектор равна:
, ограничивающей искомый сектор равна:
Нам необходимо найти при каком объем воронки (правильного конуса)
объем воронки (правильного конуса)
будет наибольшим. Запишем формулу объема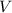 конуса:
конуса:
где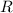 - радиус основания конуса;
- радиус основания конуса; 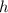 - высота конуса
- высота конуса
Поскольку длина окружности основания конуса равна , то отсюда
, то отсюда
Высоту конуса найдем с теоремы Пифагора:
Подставим в (4) вместо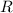 выражение (3):
выражение (3):
Подставим в (2) вместо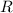 и
и 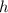 соотвественно выражения (3) и (5), получим:
соотвественно выражения (3) и (5), получим:
где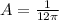
Очевидно, что естественной областью определения объема как функции от есть интервал:
есть интервал:
Продифференцируем (6) по :
:
Чтобы функция (6) имела на естественной области ее определения максимум или минимум, необходимо чтобы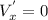 --------(9)
--------(9)
Тогда из (8) и (9) получим:
Поскольку естественной области определения (7) принадлежит только одна критическая точка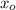 и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка
и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка 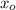 - точка максимума функции (6). Другими словами, при
- точка максимума функции (6). Другими словами, при 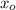 объем воронки будет наибольшим.
объем воронки будет наибольшим.
Теперь мы можем найти радианную меру искомого сектора, для чего подставим в (1) вместо критическую точку
критическую точку 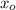 :
: