Исследуйте на чётность и нечетность функцию:
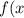$f(x) = \frac{2 \sin x}{7x^{2} + 4 }$
и функцию
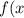$f(x) = 6x^{4} + x^{5} \cos2x \times \sin x$

Ответы

albina188 10.10.2020 13:33

Необходимые в процессе вычислений свойства:

$sin(-x)=-sinx; cos(-x)=cosx; (-x)^{2n} =x^{2n}; (-x)^{2n+1}=-x^{2n+1};$

$$f(x)=\frac{2sinx}{7x^2+4}; f(-x)=\frac{2sin(-x)}{7(-x)^2+4}=-\frac{2sinx}{7x^2+4}; f(-x)=-f(x)$

Функция нечетная

$f(x)=6x^4+x^5\cdot cos2x\cdot sinx; \\ f(-x)=6(-x)^4+(-x)^5\cdot cos(2(-x))\cdot sin(-x)= \\ =6x^4+x^5\cdot cos2x\cdot sinx; f(-x)=f(x)$

Функция четная

ПОКАЗАТЬ ОТВЕТЫ

Shady2002 10.10.2020 13:33

ответ: во вложении Пошаговое объяснение:

и функци" />

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

48096остьлмс 10.11.2020 12:40

odyvanchik22 10.11.2020 12:39

delacourr 10.11.2020 12:39

krasotkinaeliz 10.11.2020 12:39

ПОЖАЙЛУСТА ЧТОБЫ ВСЬО БЫЛО С РИСУНКОМ И ОБЯСНЕНЕМ...

санс 10.11.2020 12:39

Внести множитель под знак корня:...

Fatima82 10.11.2020 12:39

forgalaxynexusp09txz 10.11.2020 12:38

Ctatuetca 10.11.2020 12:38

agharkova2014 10.11.2020 12:38

Юлька6488262 10.11.2020 12:38

Исследуйте на чётность и нечетность функцию: и функцию​