1. Математика
  2. Исследовать сходимость

Исследовать сходимость ряда

aazzziizz aazzziizz    2   24.06.2019 17:51    0

Ответы
Damir6565 Damir6565  20.07.2020 07:51

Первый Этот ряд эквивалентен гармоническому ряду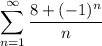 \displaystyle \sum^{\infty}_{n=1}\frac{8+(-1)^n}{n}, а так как гармонический ряд расходится, то и данный ряд тоже расходится.

Второй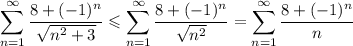 \displaystyle \sum^{\infty}_{n=1}\dfrac{8+(-1)^n}{\sqrt{n^2+3}}\leqslant\sum^{\infty}_{n=1}\dfrac{8+(-1)^n}{\sqrt{n^2}}=\sum^{\infty}_{n=1}\dfrac{8+(-1)^n}{n}

По сути ряд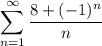 \displaystyle \sum^{\infty}_{n=1}\dfrac{8+(-1)^n}{n} - гармонический, является расходящимся, следовательно, по первому признаку сравнения данный ряд тоже является расходящимся.

ответ: ряд расходится.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
magmadi1 magmadi1  12.12.2020 01:27
Решите уравнение x:0,8=15:4​...
alexxxxarchenko alexxxxarchenko  12.12.2020 01:27
–3x + 5y–0,3x + 9,5y9,5y + 0,3x2y​...
Aynur123455 Aynur123455  12.12.2020 01:27
Найдите значение числового выражения 4х 5/18 - 1/3 х 5/6​...
Лизззззззаааааа Лизззззззаааааа  12.12.2020 01:27
Запиши следующие дроби в порядке возрастания ​...
buniatyansona buniatyansona  12.12.2020 01:27
Задание 1 Выполни умножение и деление в столбик4 603-28405 324 54​...
3848390 3848390  12.12.2020 01:26
5 Реши задачу. Два грузовика перевезли 99 тонн груза, сделав одинаковоколичество рейсов. Сколько тонн груза перевез каждыегрузовик, если один за рейс перевозил 4 тонны, а другой -5...
illaria2703 illaria2703  12.12.2020 01:26
4. Найти длину вектора AB={2,1,-5}​...
kristail2003101979 kristail2003101979  12.12.2020 01:26
Task 1 Choose the correct form of the adjectives A 1.Longer-the Don-is-the Volga than2. More-Spain-Germany-than-beautiful-is.3. Taller-are-you-than-me.4. Better-car-my-his-than-is.5.Cheaper-flowers-these-those-ones-are-than.​...
milasuraeva milasuraeva  12.12.2020 01:25
Преобразуйте смешанные числа в неправильные дроби, а неправильные дроби в смешанные числа судари и барышни. ​...
лера21091 лера21091  12.12.2020 01:25
На отрезке [0;1] случайным образом независимо друг от друга выбирают две точки х и у. Найти вероятность того, что x 0,8; y≤0,3​...

Популярные вопросы