1. Математика
  2. Исследовать ряд на сходимости

Исследовать ряд на сходимости сумма sin^2)n/n^2 +2n-1​

7Tamada7 7Tamada7    2   12.12.2019 11:57    0

Ответы
maksnovok007 maksnovok007  23.08.2020 10:56

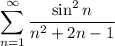
\displaystyle \sum^{\infty}_{n=1}\dfrac{\sin^2n}{n^2+2n-1}

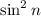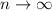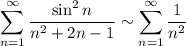\sin^2n при n\to \infty принимает значения [0;1]. Поэтому \displaystyle \sum^{\infty}_{n=1}\frac{\sin^2n}{n^2+2n-1}\sim\sum^{\infty}_{n=1}\frac{1}{n^2}. Поскольку ряд 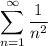\displaystyle \sum^{\infty}_{n=1}\frac{1}{n^2} сходится, то и сходится сумма ряда 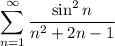\displaystyle \sum^{\infty}_{n=1}\frac{\sin^2n}{n^2+2n-1} (первый признак сравнения)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
mogilevser mogilevser  25.07.2019 19:20
Пять в минус 3 степени умножить на 5 в шестой разделить на 5 во второй степени...
ppoppo ppoppo  25.07.2019 19:20
Выбрать числовые выражения с одинаковыми уменьшаемыми...
2499930 2499930  25.07.2019 19:20
На даче растут 26 деревьев: яблони, груши и вишни. яблок составляет 50% , а вишни ⅔ числа груш. сколько деревьев каждого вида растёт в саду...
umnik84530 umnik84530  25.07.2019 19:20
Площадь участка 1200м в квадрате, со 100 м в квадрате собрали по 48 кг зерна , сколько зерна собрали со всего участка....
M7ila M7ila  25.07.2019 19:20
Водном мешке в 1.5 раза больше муки.чем в другом.после того как из первого мешка достали 35 кг муки,а из второго 17 кг,муки в обоих мешках стало поровну...
131133 131133  25.07.2019 19:20
Coднoй cтaнции oднoврeмeнно в противо положныйх направлениях вышли два поезда.скорость одного из них 56 км/ч а скрорость другого состовляет сем восьмых скорости первого...
nalimovshurik nalimovshurik  25.07.2019 19:20
Как решить уравнение 52385- икс=385...
Danielllllllll Danielllllllll  25.07.2019 19:20
Удимы в копилке 240рублей .он может купить на них 3 книги по одной цене или 4одинаковых альбома .на сколько альбом дешевле книги?...
tanyabober tanyabober  25.07.2019 19:20
На рынке продали баранину и телятину причём баранины 13 грамм больше чем телятина стоимость проданной мясо если известно что масса баранины относится к мастер резина...
Nesty111111 Nesty111111  25.07.2019 19:20
Действия этого примера 564*70-564*60...

Популярные вопросы