1. Математика
  2. Исследовать ряд на сходимость;

Исследовать ряд на сходимость; если сходиться, то абсолютно или условно.нужно.

vvv76 vvv76    3   24.12.2019 18:33    0

Ответы
zswdfx zswdfx  10.10.2020 23:03

(\dfrac{1}{\sqrt{n+7}})'=-\dfrac{1}{n+7}\cdot \dfrac{1}{2\sqrt{n+7}}, а значит члены ряда \sum \dfrac{(-1)^{n+1}}{\sqrt{n+7}} убывают по модулю. А значит, т.к. ряд знакочередующийся, ряд сходится по признаку Лейбница.

Теперь рассмотрим ряд из модулей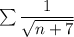 \sum \dfrac{1}{\sqrt{n+7}}.

\dfrac{1}{\sqrt{n+7}} \dfrac{1}{(8n)^\frac{1}{2}}\\ \sum \dfrac{1}{(8n)^\frac{1}{2}}

расходится по степенному признаку. Тогда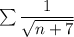 \sum \dfrac{1}{\sqrt{n+7}} расходится по признаку сравнения.

Значит исходный ряд сходится условно

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
adidas128 adidas128  02.08.2019 02:00
Какие цифры можно поставить вместо звёздочки,чтобы получилось верное неравенство? а)34*7 3487 б)1*785 10898 в)*0354 79531 г)59672 5*772 д)50314 5*3*3 е)6*783 607*1 ж)7*2*9...
milashka44 milashka44  02.08.2019 02:00
По татарскому языку. попросить у друга тетрадь и ручку...
misszhilinskay misszhilinskay  02.08.2019 02:00
Маршрут велосипедного пробега 120 километра.горизонтальный участок составляет 60 процентов всего пути , подъём - 1/8 всего пути, а остальная его часть имеет уклон. сколько...
Meluran Meluran  02.08.2019 02:00
2в квадрате +3 в квадрате сколько будет?...
Karon1337 Karon1337  02.08.2019 02:00
Вдвух бригадах 47 человек.в 1-ой бригаде неизвестно рабочих,а во 2-ой на 7 больше чем в первой.сколько в первой и во второй бригаде рабочих...
Jeembo23 Jeembo23  02.08.2019 02:00
Решите : в хоре 80 учащихся,1/4 из них-мальчики. сколько мальчиков в хоре? 2 : мальчик собрал 80 орехов, что составляет 2/3 всех собранных орехов. сколько орехов было...
biolev biolev  02.08.2019 02:00
Может ли число в записи которого все цыфры 2 делиться на целое число в записи которого все цифры равны 1) 1, 2) 5...
dabushov95 dabushov95  02.08.2019 02:00
Вороне где-то бог послал кусочек сыра, в нем содержалось 45% жира белка же было 35 хотели б массу сыра мы узнать, но только знаем с вами мы пока, что жира было в нем...
vikaberg vikaberg  02.08.2019 02:00
X-3,2=две целых 7 15 x+5,65=7,8 4 целых 7 12-у=2,5...
julyazolotko20 julyazolotko20  02.08.2019 02:00
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия....

Популярные вопросы