исследовать несобственные интегралы на сходимость, пример: 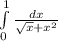 . ответ: совпадает
. ответ: совпадает
Другие вопросы по теме Математика
Популярные вопросы
- Запиши выражения в которых разность двух чисел равна нулю произведение...
2 - Являются ли линейными функции заданные формулами: y=6x-1...
2 - Найдите последнюю цифру числа! 1! +2! ++2015! (n-произведение всех...
2 - Для плавления 2 кг меди,взятой при тем-ре плавления требуется кол-во...
3 - Чему радовалась роза? как она выражала свои чувства? подчеркните...
1 - ответьте на вопросы на языке: 1.when does school begin in russia?...
3 - Состав крови малого круга и большого круга кровообращения...
3 - 4.прочитай слова. какую букву надо написать на месте .подберии запиши...
1 - Почему необходимо поддерживать постоянное движение крови?...
1 - Найти значение выражения 6003*(24396: 76-319+26)...
2
интеграл сходится
Пошаговое объяснение:
Найдем соответствующий неопределенный интеграл:
________________________________
Разложим дробь на сумму простейших:
________________________________
Вычислим несобственный интеграл:
Интеграл сходится
Сходится
Пошаговое объяснение:
Одна особая точка: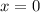
Значит, по степенному признаку, исходный интеграл сходится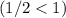 .
.