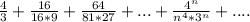 Исследовать на сходимость ряд
Исследовать на сходимость ряд
Другие вопросы по теме Математика
Популярные вопросы
- Напиши глаголы в полной форме. образец: she isn t in year 2. she is...
3 - Речення з фразеологізмами мудра голова ,сильна сторона ,гостре слово....
3 - Составе план по сказке сказка о молодильных яблоках и живой воде...
3 - Надо решить уравнение (y-152)•59=6018...
2 - Скинте чертёж цистерны 4 класс роговцева....
1 - Дано: u1 = 1,5 м/c t1 = 2ч s2 = 2км t2 = 1ч u ср -? кто нибудь завтра...
3 - Подумать предложение со словам хлеб в разных значениях...
1 - Начертите развернутый угол еок. проведите биссектрису of. сколько градусов...
2 - Встарших классах школы 780 учащихся сколько человек от этого количества...
2 - На уроке (гл. слово уроке), начало урока(гл.слово начало), читает книгу(гл....
2
По признаку Даламбера ряд расходится.