1. Математика
  2. Исследовать на сходимость

Исследовать на сходимость ряд

Nastasia8879 Nastasia8879    2   15.12.2019 17:14    1

Ответы
Brosherin Brosherin  10.10.2020 20:46

\sum^{\infty}_{n=1}\dfrac{3-n}{n^2+5n+7}=\dfrac{2}{13}+\dfrac{1}{21}+0-\sum^{\infty}_{n=4}\dfrac{n-3}{n^2+5n+7}\\ \sum^{\infty}_{n=4}\dfrac{n-3}{n^2+5n+7}=[k=n-3]=\sum^{\infty}_{k=1}\dfrac{k}{k^2+11k+31}\geq [11k+31\leq 42k^2\: \forall k \geq 1] \geq \sum^{\infty}_{k=1}\dfrac{k}{43k^2}=\dfrac{1}{43}\sum^{\infty}_{k=1}\dfrac{1}{k}

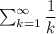\sum^{\infty}_{k=1}\dfrac{1}{k} - гармонический ряд, он расходится. Тогда, по признаку сравнения, расходится и ряд 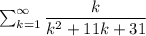\sum^{\infty}_{k=1}\dfrac{k}{k^2+11k+31}. Добавление к ряду конечного числа конечных членов не влияет на его сходимость, а значит и исходный ряд расходится

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Turalinin Turalinin  26.11.2019 18:31
Исследовать функцию и построить график y=(2)/(x^2+2x)​...
zuza81ozzhmr zuza81ozzhmr  26.11.2019 18:31
Если вычесть одно от другого то получится 142,а сумма чисел равна 832.!...
Дашенька66778 Дашенька66778  26.11.2019 18:31
Обчисліть об’єм куба з ребром 7 см...
Sofiko20017 Sofiko20017  26.11.2019 18:33
Часы показывают 12: 20. найдите угол между их стрелками. решите !...
darkhanio darkhanio  26.11.2019 18:33
Решить(с подробным объяснением)...
JoshuaJoseph JoshuaJoseph  26.11.2019 18:33
Теорія ймовірностей нужно. . 4.6...
рубін рубін  26.11.2019 18:35
Представьте в виде суммы или разности произведения, (a+c)* 64.3...
aselkulmagambet aselkulmagambet  26.11.2019 17:11
Марья-искусница вышила жемчугом платки на 4 платка у неё ушло 80 жемчужин поровну на каждый платок сколько жемчужин нужно для 5 таких платков...
Миша1112994 Миша1112994  26.11.2019 17:11
3классзапиши кружки такие знаки арифметически действий чтобы получились верные примеры: 18 =1618 =6...
SQQQUAD SQQQUAD  26.11.2019 17:12
Протяжённость маршрута - 480 км. туристы совершают поездку на автомобиле. они проехали 2 часа со скоростью 85 км/ч можете ещё краткую запись скинуть? ​...

Популярные вопросы