Исследовать и найти общее решение системы линейных однородных
уравнений.

Ответы

nastya06nastik 04.10.2020 09:56

$x_1-3x_2-4x_3+x_4=0\\5x_1-8x_2-2x_3+x_4=0\\-2x_1-x_2-10x+3-5x_4=0$

1. Согласно теореме Кронекера-Капелли будем искать ранги соответствующих матриц, пока не найдем базис.

$\left[\begin{array}{ccc}1\end{array}\right] = 1 \neq 0$

$\left[\begin{array}{ccc}1&-3\\5&-8\end{array}\right] = -8 + 15 = 7 \neq 0$

$\left[\begin{array}{ccc}1&-3&-4\\5&-8&-2\\-2&-1&-10\end{array}\right] = (-8)(-10) + (-3)(-2)(-2)+5(-4)(-1) - ((-4)(-8)(-2)+5(-3)(-10)+(-1)(-2)) = 0$

Оп, определитель равен нулю. В точности такой же, как и расширенной матрицы. Значит,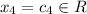 $x_4=c_4\in R$

Перепишем упрощенную систему:

$x_1-3x_2-4x_3+c_4=0\\5x_1-8x_2-2x_3+c_4=0\\-2x_1-x_2-10x_3-5c_4=0$

Из первого уравнения выразим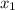 x_1 :

$x_1=3x_2+4x_3-c_4\\5x_1-8x_2-2x_3+c_4=0\\-2x_1-x_2-10x_3-5c_4=0$

Теперь подставим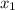 x_1 во второе уравнение СЛАУ:

$x_1=3x_2+4x_3-c_4\\5(3x_2+4x_3-c_4)-8x_2-2x_3+c_4=0\\-2(3x_2+4x_3-c_4)-x_2-10x_3-5c_4=0\\- - - - - - - - - - - - - - - - - - -\\x_1=3x_2+4x_3-c_4\\15x_2+20x_3-5c_4-8x_2-2x_3+c_4=0\\-6x_2-8x_3+2c_4-x_2-10x_3-5c_4=0\\- - - - - - - - - - - - - - - - - - -\\x_1=3x_2+4x_3-c_4\\7x_2+18x_3-4c_4=0\\-7x_2-18x_3-3c_4=0\\- - - - - - - - - - - - - - - - - - -\\x_1=3x_2+4x_3-c_4\\7x_2+18x_3-4c_4 + (-7x_2-18x_3-3c_4) =0\\-7x_2-18x_3-3c_4=0\\- - - - - - - - - - - - - - - - - - -$

$x_1=3x_2+4x_3-c_4\\-7c_4=0 =c_4=0\\-7x_2-18x_3-3c_4=0\\- - - - - - - - - - - - - - - - - - -\\x_1=3x_2+4x_3-0\\7x_2+18x_3-4*0 =0\\-7x_2-18x_3-3*0=0\\- - - - - - - - - - - - - - - - - - -\\x_1=3x_2+4x_3\\7x_2 = -18x_3 = x_2 = -\frac{18}{7}x_3\\\\--------------------\\$