Исследовать функцию y=x^3-x^2 и построить график
Ответы
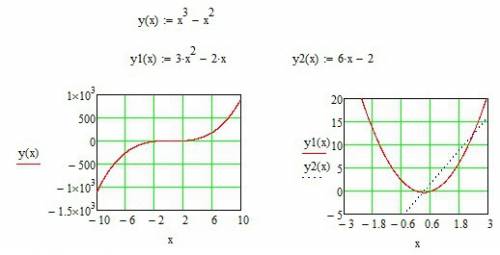
Определим первую производную функции y1(x)=3*x²-2*x. Далее находим, при каких х функция равна нулю. Решаем квадратное уравнение. x1=0, x2=0.667. В точке х1 производная меняет знак с + на -, это точка локального максимума. В точке х2 производная меняет знак с - на +, это точка локального минимума. Определим 2 производную y2(x)=6*x-2. y2 равна нулю при х=0,333. То есть левее точки 0,333 исходная функция имеет выпуклость вверх (y2 отрицательна ), а правее выпуклость вниз (y2 положительна). Графики приложены в рисунке.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика
Популярные вопросы
- Введите IP-адрес сервера с доменным именем С РЕШЕНИЕМ. У МЕНЯ НЕТ...
1 - Сколько существует прямоугольников с площадью 48?...
1 - Мне начинает казаться,что я вдруг стал великаном,и всё моё существо...
2 - Какие нормы являются самыми древними: А) религиозные нормы Б) нормы...
2 - √3sin x =2 розв яжіть рівняння...
3 - Два тіла, маси яких однакові і рівні 100 г, зв язані ниткою, лежать...
1 - Записать уравнение альфа распада для фтора - 17. Посчитать энергетический...
3 - Выдели признаки, характерные для жизни широкого лентеца в живом организме...
1 - 218. Восстановите целостность неопределённых местоимений. Об-ясните...
3 - Найдите координаты середины отрезка BC если B(3;2) C(-1;6)...
2