Исследование функции надо провести, первые 6 пунктов, с графиком. ВОТ ПУНKТЫ:
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
1−x=0,⇒x=1.
Исключаем единственную точку x=1 из области определения функции и получаем:
D(y)=(−∞;1)∪(1;+∞).
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка x=1 является разрывом второго рода, прямая x=1 - вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат Oy, для чего приравниваем x=0:
Таким образом, точка пересечения с осью Oy имеет координаты (0;8).
Найдем точки пересечения с осью абсцисс Ox, для чего положим y=0:
Уравнение не имеет корней, поэтому точек пересечения с осью Ox нет.
Заметим, что x2+8>0 для любых x. Поэтому при x∈(−∞;1) функция y>0 (принимает положительные значения, график находится выше оси абсцисс), при x∈(1;+∞) функция y 0, функция возрастает на данных промежутках.
При этом x=−2 - точка локального минимума (функция убывает, а потом возрастает), x=4 - точка локального максимума (функция возрастает, а потом убывает).
Скиньте решение на фото
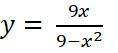
Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Популярные вопросы
- Провідміняти дев’яносто шість(будуть паралельні форми)...
2 - Селдің қасиеттерін зерттеу тәжірибесі...
1 - проанализируйте таблицу два самых сильных электролитов и Обоснуйте...
1 - с геометрией 8 класс! заранее благодарен...
2 - 2) Түркістан-ежелгі қала тақырыбында сабақта алған мәліметтеріңізге...
1 - Определить сумму двоичных чисел 11101010011.111+1111100101.011...
3 - Солтүстік Қазақстанның орманды даласында бұғы, елік, ақ қояндар кездеседі....
3 - Задано поштову електронну адресу uruge mall.unicrosoft.com. Який лосін...
3 - Выручайте! Физика, посчитать общее сопротивление...
2 - Во всех случаях у флориста будет еще 2 цветка в одном букете, будь...
2