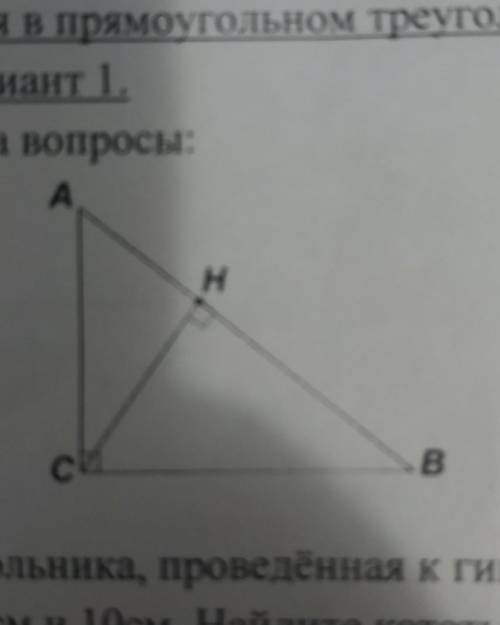
Используя рисунок, ответьте на вопросы: 1) ∆АНС ~ ∆...
2) СН² = ...
3) ВС² = ...
4) Найти CH, AC и BC,
если AH=16,HB=25​

Чтобы ответить на эти вопросы, давайте разберемся с рисунком и воспользуемся некоторыми определениями и свойствами треугольников.

1) Для ответа на первый вопрос, мы сравним треугольники ∆АНС и другие треугольники на рисунке. Из рисунка видно, что углы ∠А и ∠С прямые, следовательно, треугольник АСН прямоугольный. По определению, прямоугольный треугольник имеет один угол в 90 градусов.

Теперь давайте сравним стороны треугольников. Из рисунка видно, что сторона АН у треугольника АНС является гипотенузой прямоугольного треугольника. АН также является стороной треугольника АСН. Таким образом, мы можем сказать, что треугольники ∆АНС и ∆АСН подобны.

2) Чтобы найти значение СН², мы можем использовать теорему Пифагора в прямоугольном треугольнике АСН.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, мы имеем катет СH равным 16 и гипотенузу СН, которую мы пытаемся найти. Таким образом, мы можем записать это в виде уравнения:

СH² + AH² = СН²

Подставляем известные значения:

16² + 25² = СН²

256 + 625 = СН²

881 = СН²

Поэтому, СН² = 881.

3) Аналогично, чтобы найти значение ВС², мы можем использовать теорему Пифагора в прямоугольном треугольнике ВСН.

ВС является гипотенузой прямоугольного треугольника ВСН. Мы знаем, что ВH = AH + BH = 16 + 25 = 41, а CH = 16. Подставляем известные значения в уравнение теоремы Пифагора:

ВС² = ВH² + CH² = 41² + 16² = 1681 + 256 = 1937.

Поэтому, ВС² = 1937.

4) Чтобы найти длины сторон CH, AC и BC, давайте рассмотрим отрезки на рисунке.

Мы уже знаем, что CH = 16 и ВС² = 1937. Для нахождения длины ВС, мы возьмем квадратный корень из ВС²:

ВС = √1937.

Также мы можем использовать теорему Пифагора в треугольнике АСН для нахождения длины AC:

AH² + CH² = AC².

Подставляем известные значения:

16² + 16² = AC².

256 + 256 = AC².

AC² = 512.

AC = √512.

Наконец, длина BC можно найти, используя разность длины ВС и AC:

BC = ВС - AC.

Теперь вы можете использовать калькулятор, чтобы найти значения ВС, AC и BC, проверив свои ответы. Убедитесь, что используете округленные значения квадратных корней, если требуется.