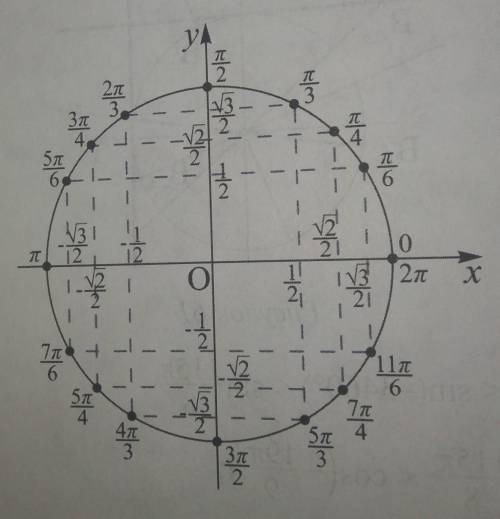
Используя рисунок найдите синус а, косинус а, тангенс а, котангенс а угла а, равного: - 30,-45,-60,210,225,240 градусов​

Хорошо! Давайте решим эту задачу пошагово.

Для начала, давайте разберемся в основных понятиях. В треугольнике ABC (как показано на рисунке), угол a противоположен стороне AC. В данном случае, сторона AC является гипотенузой, сторона AB - прилежащей катетом, а сторона BC - противоположным катетом.

Теперь, давайте найдем синус, косинус, тангенс и котангенс угла a для заданных значений.

1. Для угла -30 градусов:
Сначала найдем соответствующую сторону, которая соответствует углу -30 градусов. Похоже, что сторона AB соответствует этому углу. Заметим, что сторона AB равна 1 (так как это равносторонний треугольник).

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла -30 градусов:
sin(-30) = противоположная сторона / гипотенуза
= AB / AC
= 1 / 2
= 1/2

- Косинус угла -30 градусов:
cos(-30) = прилежащая сторона / гипотенуза
= BC / AC
= √3 / 2 (так как BC = √3)
= √3/2

- Тангенс угла -30 градусов:
tan(-30) = противоположная сторона / прилежащая сторона
= AB / BC
= 1 / √3
= √3/3

- Котангенс угла -30 градусов:
cot(-30) = 1 / tan(-30)
= 1 / (√3/3)
= 3 / √3
= √3

Таким образом, для угла -30 градусов мы получаем:
sin(-30) = 1/2
cos(-30) = √3/2
tan(-30) = √3/3
cot(-30) = √3

2. Для угла -45 градусов:
В данном случае, сторона AB является прилежащим катетом. Заметим, что сторона AB равна 1 (так как это равносторонний треугольник).

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла -45 градусов:
sin(-45) = противоположная сторона / гипотенуза
= AC / AC
= 1

- Косинус угла -45 градусов:
cos(-45) = прилежащая сторона / гипотенуза
= AB / AC
= 1 / √2 (так как AB = 1 и AC = √2)
= √2/2

- Тангенс угла -45 градусов:
tan(-45) = противоположная сторона / прилежащая сторона
= AC / AB
= 1 / 1
= 1

- Котангенс угла -45 градусов:
cot(-45) = 1 / tan(-45)
= 1 / 1
= 1

Таким образом, для угла -45 градусов мы получаем:
sin(-45) = 1
cos(-45) = √2/2
tan(-45) = 1
cot(-45) = 1

3. Для угла -60 градусов:
В данном случае, сторона AB является противоположным катетом. Заметим, что сторона AB равна 1 (так как это равносторонний треугольник).

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла -60 градусов:
sin(-60) = противоположная сторона / гипотенуза
= AB / AC
= 1 / 2
= 1/2

- Косинус угла -60 градусов:
cos(-60) = прилежащая сторона / гипотенуза
= BC / AC
= 1 / 2
= 1/2

- Тангенс угла -60 градусов:
tan(-60) = противоположная сторона / прилежащая сторона
= AB / BC
= 1 / 1
= 1

- Котангенс угла -60 градусов:
cot(-60) = 1 / tan(-60)
= 1 / 1
= 1

Таким образом, для угла -60 градусов мы получаем:
sin(-60) = 1/2
cos(-60) = 1/2
tan(-60) = 1
cot(-60) = 1

4. Для угла 210 градусов:
Для угла 210 градусов, взглянем на треугольник FGH. Заметим, что сторона GH является прилежащим катетом, а сторона FG - противоположным катетом.

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла 210 градусов:
sin(210) = противоположная сторона / гипотенуза
= FG / AC
= -√3 / 2 (так как FG = -√3 и AC = 2)
= -√3/2

- Косинус угла 210 градусов:
cos(210) = прилежащая сторона / гипотенуза
= GH / AC
= -1 / 2 (так как GH = -1 и AC = 2)
= -1/2

- Тангенс угла 210 градусов:
tan(210) = противоположная сторона / прилежащая сторона
= FG / GH
= -√3 / -1
= √3

- Котангенс угла 210 градусов:
cot(210) = 1 / tan(210)
= 1 / √3
= √3/3

Таким образом, для угла 210 градусов мы получаем:
sin(210) = -√3/2
cos(210) = -1/2
tan(210) = √3
cot(210) = √3/3

5. Для угла 225 градусов:
Для угла 225 градусов, взглянем на треугольник IJK. Заметим, что сторона KJ является прилежащим катетом, а сторона JK - противоположным катетом.

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла 225 градусов:
sin(225) = противоположная сторона / гипотенуза
= JK / AC
= -1 / √2 (так как JK = -1 и AC = √2)
= -1/√2

- Косинус угла 225 градусов:
cos(225) = прилежащая сторона / гипотенуза
= KJ / AC
= -1 / √2 (так как KJ = -1 и AC = √2)
= -1/√2

- Тангенс угла 225 градусов:
tan(225) = противоположная сторона / прилежащая сторона
= JK / KJ
= -1 / -1
= 1

- Котангенс угла 225 градусов:
cot(225) = 1 / tan(225)
= 1 / 1
= 1

Таким образом, для угла 225 градусов мы получаем:
sin(225) = -1/√2
cos(225) = -1/√2
tan(225) = 1
cot(225) = 1

6. Для угла 240 градусов:
Для угла 240 градусов, взглянем на треугольник LMN. Заметим, что сторона MN является прилежащим катетом, а сторона LN - противоположным катетом.

Теперь, найдем значения синуса, косинуса, тангенса и котангенса:
- Синус угла 240 градусов:
sin(240) = противоположная сторона / гипотенуза
= LN / AC
= -√3 / 2 (так как LN = -√3 и AC = 2)
= -√3/2

- Косинус угла 240 градусов:
cos(240) = прилежащая сторона / гипотенуза
= MN / AC
= -1 / 2 (так как MN = -1 и AC = 2)
= -1/2

- Тангенс угла 240 градусов:
tan(240) = противоположная сторона / прилежащая сторона
= LN / MN
= -√3 / -1
= √3

- Котангенс угла 240 градусов:
cot(240) = 1 / tan(240)
= 1 / √3
= √3/3

Таким образом, для угла 240 градусов мы получаем:
sin(240) = -√3/2
cos(240) = -1/2
tan(240) = √3
cot(240) = √3/3

Надеюсь, что эти пошаговые решения помогут вам разобраться в нахождении синуса, косинуса, тангенса и котангенса для заданных углов. Если у вас возникнут еще какие-либо вопросы, не стесняйтесь задавать их.