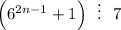Используя метод индукции, докажите, что для любого натурального числа n истины утверждения:
Другие вопросы по теме Математика
Популярные вопросы
- Куски олова и свинца с одинаковой высоты. у какого из металлов в результате падения...
1 - Три стрелка поражают цель с вероятностями 1 ый 0.6 2 й 0.81 3тий 0.95 найдите...
3 - Укажите лишнее (по разряду): 1) сам 2) самый 3) всякий 4) каждый 5) мой...
2 - Что и для кого строили в древней руси...
3 - 1)что такое агарозный электрофорез? 2)что такое днк растений ? 3)как классифицировать...
2 - Решить хотя бы одну , надо № 7 как изменится строение белка, если в молекуле...
1 - Решить хотя бы одну , № 4 в семье трое детей и все имеют кровь разной группы:...
3 - Television ,tim,watch,never составить предложение...
1 - Вставь пропущенные буквы (двойные согласные) держи , пока в руках, а выпустил-...
1 - (8x-12)(8x+12)-64x^2+6x+45приx=140 решите , надо...
3
Используя метод математической индукции, докажите, что для любого натурального числа n истины утверждения: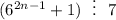
1) Базис индукции: n = 1
2) Предположим что и при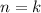 выражение
выражение 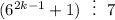
3) Индукционный переход: n = k + 1.
Первое слагаемое делится на 7 по предположению (второй пункт), ну а второе слагаемое очевидно, что 35 : 7, значит и все выражение делится на 7. Следовательно, для всех натуральных n выражение