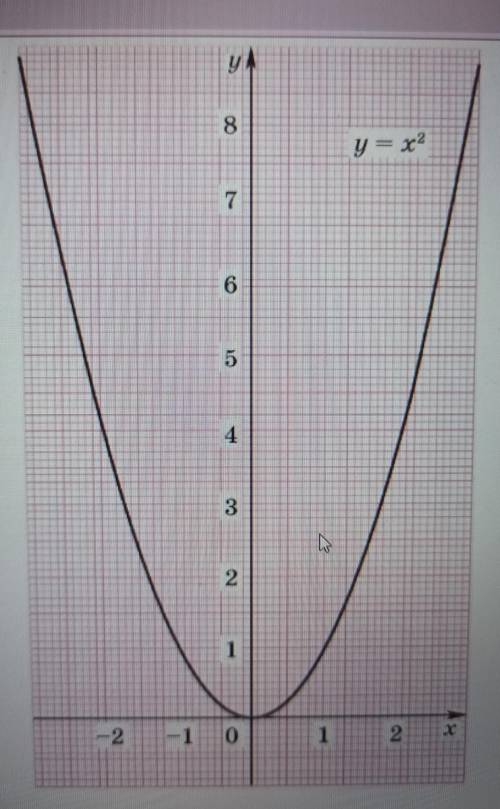
Используя график функции y=x^2 реши уравнение: если корней несколько, запиши их в порядке возрастания через точку с запятой.

а) x^2=2x+3, x=
б) x^2+x+3=0, x=
ОЧЕНЬ

Добро пожаловать в нашу школу! С удовольствием помогу тебе решить эти уравнения, используя график функции y=x^2.

a) Уравнение x^2=2x+3. Для начала, перенесем все члены уравнения в одну сторону: x^2-2x-3=0. Затем, посмотрим на график функции y=x^2 и найдем точки пересечения графика с осью x. На графике видно, что у функции есть два пересечения с осью x: одно в районе x=-1 и второе в районе x=3.

Теперь мы найдем координаты точки пересечения функции y=x^2 с прямой y=2x+3. Подставим уравнение прямой в уравнение функции и решим его. Получаем x^2=2x+3: x^2-2x-3=0.

Мы знаем, что одно из пересечений графиков находится в x=-1. Подставим эту координату в уравнение прямоугольника: (-1)^2-2*(-1)-3=1+2-3=0. Оно равно 0, поэтому x=-1 является одним из корней уравнения.

Теперь найдем второй корень. Подставим в уравнение прямой вторую координату пересечения графиков, x=3: (3)^2-2*(3)-3=9-6-3=0. Второй корень уравнения равен x=3.

Итак, мы получили два корня уравнения x^2=2x+3: x=-1 и x=3.

б) Уравнение x^2+x+3=0. Поступим аналогичным образом для решения этого уравнения. Перенесем все члены в одну сторону: x^2+x+3=0. Посмотрим на график функции y=x^2 и найдем точки пересечения графика с осью x. На графике видно, что график функции y=x^2 никогда не пересекает ось x, поэтому у этого уравнения нет действительных корней.

Мы можем доказать это, решив уравнение x^2+x+3=0 методом дискриминанта. Дискриминант D для этого уравнения равен D=1^2-4*1*3=-11, что отрицательно. Поскольку дискриминант меньше нуля, уравнение не имеет действительных корней.

Таким образом, уравнение x^2+x+3=0 не имеет корней.

Надеюсь, я смог ответить на твой вопрос об использовании графика функции y=x^2 для решения уравнений. Если у тебя остались какие-либо вопросы, я с удовольствием помогу!