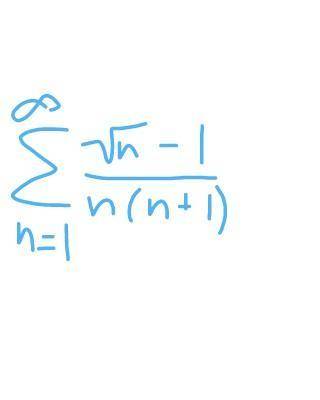
Математика: Иследовать ряд на сходимость, но не через Дирихле

Иследовать ряд на сходимость, но не через Дирихле

Ответы

левецинкking 09.07.2021 21:50

Как применять здесь признак Дирихле, я не придумал. Хорошо, что автор задания не разрешил пользоваться им)). А может быть автор имеет в виду, что нельзя использовать знание, при каких значениях параметра ряд Дирихле сходится, а при каких расходится? Ну не будем, так и быть. Но если ряд Дирихле случайно появится, мы не виноваты, и даже будем делать вид, что не узнали его.

Воспользуемся признаком сравнения:

$0\le a_n=\frac{\sqrt{n}-1}{n(n+1)}\le b_n=\frac{\sqrt{n}}{n^2}=\frac{1}{n^{3/2}}=n^{-3/2}.$

Докажем, что ряд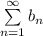 $\sum\limits_{n=1}^{\infty}b_n$ сходится. Докажем это с интегрального признака Коши. Монотонное убывание функции

$f(x)=\frac{1}{x^{3/2}}$ при $x\in [1;+\infty)$ очевидно (если не верите - посчитайте производную). Обычно требуют сделать проверку стремления f(x) к нулю на плюс бесконечности, но на самом деле признак работает и без этого условия (другое дело, если функция не стремится к нулю, расходимость ряда очевидна и без всякого признака). Но если Вас это напрягает - посмотрите на функцию и у Вас не будет никаких сомнений в стремлении ее к нулю. Остается исследовать несобственный интеграл

$\int\limits_1^{\infty} \frac{dx}{x^{3/2}}$ на сходимость.

$\int\limits_1^{\infty}x^{-3/2}\, dx=\left. \frac{x^{-1/2}}{-1/2}\right|_1^{\infty}=-2(\lim\limits_{x\to +\infty}\frac{1}{\sqrt{x}}-1)=2$

то есть интеграл сходится, а тогда и ряд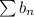 $\sum b_n$ (неужели это ряд Дирихле? вот сюрприз!) сходится, а тогда и ряд 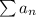$\sum a_n$ сходится по признаку сравнения.