Математика: Иследование функции с производной y=x^3-3x^2-2

Иследование функции с производной y=x^3-3x^2-2

Ответы

ytxrgh 20.07.2020 08:51

1. Функция монотонная (все слагаемые функции являются монотонными (непрерывными) функциями).

2. $y'(x) = 3x^2-6x\\3x^2-6x=0\\3x(x-2)=0\\3x=0 || x-2 = 0\\x=0||x=2$

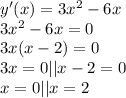
Это точки, где функция меняет свое направление (производная меняет знак), рассмотрим три интервала:

Интервал (-∞;0): возьмем любую точку из этого интервала и подставим в уравнение производной, чтобы узнать убывает или возрастает функция на этом участке:

y'(-1)=3*(-1)^2-6*(-1)=3+6=90 - функция возрастает на этом интервале

Интервал (0;2):

y'(1)=3*1^2-6*1=3-6=-3 функция убывает на этом интервале.

Интервал (2;+∞):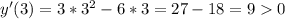 y'(3)=3*3^2-6*3=27-18=90 функция возрастает на этом интервале.

Так как в точке 0 функция меняет свой знак с положительного на отрицательный, то точка 0 - это локальный максимум функции. В точке 2 функция меняет знак с отрицательного на положительный, то есть заканчивает убывать и начинает возрастать, следовательно точка 2 - локальный минимум.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика