1. Математика
  2. Иследовафункции на прерывностьи

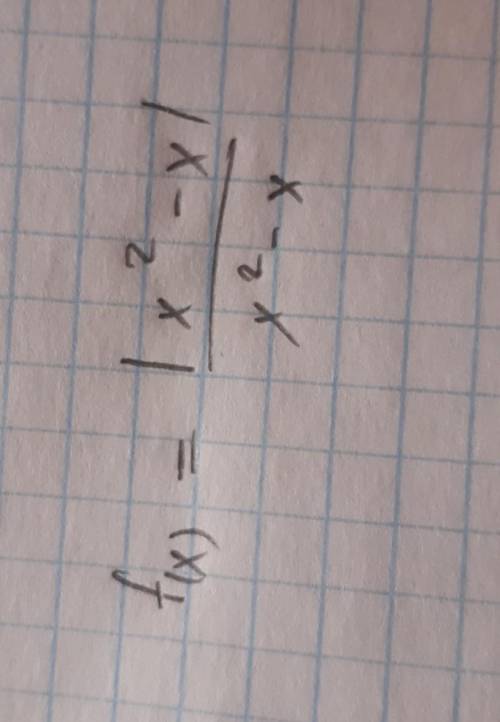
Иследовафункции на прерывностьи точки разрыва​


Иследовафункции на прерывностьи точки разрыва​

LiiiiiiV LiiiiiiV    1   06.11.2020 23:28    0

Ответы
арсений201 арсений201  06.12.2020 23:30
ответ:функция не является непрерывной, в точке х = 0 и х = 1 терпит разрывы первого рода Пошаговое объяснение:Разрыв гарантированно будет в точках где знаменатель равен 0. x^2-x=0\\x(x-1)=0\\\left[\begin{array}{ccc}x=0\\x=1\end{array}\right.

то есть рассматривать будем эти две точки

1. Рассмотрим точку х = 0

1. Тут гарантированно разрыв - делим на 0

2. вычислим односторонние пределы

\displaystyle \lim_{x\to0-0} \dfrac{|x^2-x|}{x^2-x}=\lim_{x\to0-0}\dfrac{x^2-x}{x^2-x}=1

\displaystyle \lim_{x\to0+0} \dfrac{|x^2-x|}{x^2-x}=\lim_{x\to0+0}\dfrac{-x^2+x}{x^2-x}=-1

Разрыв "скачок" - разрыв первого рода

2. Рассмотрим точку х = 1

\displaystyle \lim_{x\to1-0} \dfrac{|x^2-x|}{x^2-x}=-1

\displaystyle \lim_{x\to1+0} \dfrac{|x^2-x|}{x^2-x}=1

Тоже самое

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
KrIs1girl KrIs1girl  18.03.2019 11:30
Правильно записать условие : в парке посадили ясеней, 30 кленов, а лип столько, сколько ясеней и кленов вместе. сколько лип посадили в парке, сколько всего деревьев...
voegrogo5523 voegrogo5523  18.03.2019 11:20
Найдите числа,обратные числам 11 11 11...
nastyamashkina12 nastyamashkina12  18.03.2019 11:20
Из 100 кг винограда получилось 25 кг изюма. какую часть составляет испарившаяся вода. выразите часть в процентах...
Nahchik Nahchik  18.03.2019 11:20
Длина стороны квадрата равна 125 см. вычисли периметр этого квадрата....
аслансосланов аслансосланов  18.03.2019 11:20
Периметр треугольника равен 194дм.первая его сторона равна 70 дм,а вторая на 12 дм меньше первой .на сколько дециметров третья сторона меньше суммы первых двух?...
boykorostik boykorostik  18.03.2019 11:20
Напишите транскрипцию французских звуков по как их читать...
МамкаДраконов МамкаДраконов  18.03.2019 11:20
Напиши двузначное число, где число десятков больше на 2, чем число единиц. ( больше в 2 раза)...
Viper397 Viper397  18.03.2019 11:20
Впарке дуб был посажен на 84 года раньше сосны.сколько лет каждому дереву если возраст сосны составляет 60% дуба?...
Poniy11 Poniy11  18.03.2019 11:20
8карандашей стоит 24 руб. 2) сколько стоят 7 карандашей? 2) сколько таких карандашей может купить света, если у нее только 20 руб? сколько ей должы дать сдачи?...
dinnaasv dinnaasv  18.03.2019 11:20
Произведение трёх множителей 2772. первый наибольшое двухзначное число.второй в 29 раз больше первого.найди третий множитель....

Популярные вопросы