Исходя из определения производной, вычислить производную функции 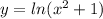
Другие вопросы по теме Математика
Популярные вопросы
- К музыкальному направлению хип-хопа относится рэп ,к изобразительному...
2 - Построить как в приведено в примере предложение из приведённых групп...
1 - дам за 3 во Там первые и последние фотки, это одно задание.)...
2 - 1. Під час зустрічі випускників ліцею 19 жовтня 1825 року Пушкін був:...
3 - Переведите в косвенную речь 1“I don’t like talking about unnecessary...
1 - У циліндрі під поршнем міститься 2 моль деякого газу. Яку роботу виконає...
3 - Как правильно ухаживать за фиалками МЕНЯ ЖДУТТТ...
3 - Чий портрет мріяв намалювати Юлько? у творі Шпага Славки Беркути ...
2 - Разберите слово,, принадлежавшей,, по морфологическому разбору И слово...
1 - Вычислить sin ( -1845 градусов), cos 3990градусов, tan (-1500градусов)...
1
ответ: y'=2*x/(x²+1)
Пошаговое объяснение:
y'=lim [y(x+Δx)-y(x)]/Δx при Δx⇒0. Но y(x+Δx)=ln[(x+Δx)²+1]=ln[x²+2*x*Δx+(Δx)²+1], поэтому y(x+Δx)-y(x)=ln[(x²+2*x*Δx+(Δx)²+1)/(x²+1)]=ln[1+(2*x*Δx+(Δx)²)/(x²+1)]. Но при Δx⇒0 бесконечно малая величина ln[1+(2*x*Δx+(Δx)²)/(x²+1)] эквивалентна бесконечно малой величине (2*x*Δx+(Δx)²)/(x²+1), поэтому Δy/Δx~[2*x*Δx+(Δx)²]/[Δx*(x²+1)]=(2*x+Δx)/(x²+1). Отсюда y'=lim(Δy/Δx)=2*x/(x²+1).