Интеграл пи на 12 dx sin2(x+пи/6) dx.
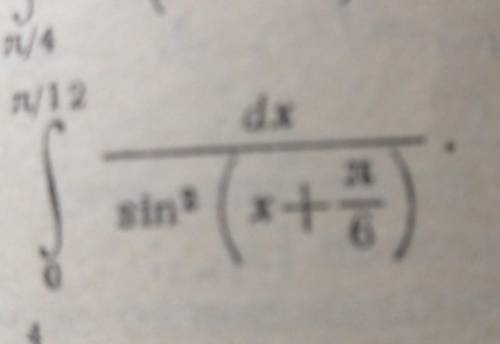
Другие вопросы по теме Математика
Популярные вопросы
- Кэрим Тинчуриннын Искэндэр дигэн хикэясендэ топ проблема нэрсэ?...
3 - І 9 больше нечево ненада заранее дякую якщощо...
2 - ХЕЛП Перечислите систематические отличия классов брюхоногих,...
2 - Визначте твори мистецтва в стилі модерн і схарактеризуйте творчість...
2 - Кто такой Егор Крид❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔❔...
3 - Контрольная по химии. В первом только А...
1 - Точки A, B, C, D розмещены на кругу так, что АВ=ВС=САВD- бисектриса...
3 - Найди значения выражений: 3 7/20:(3 2/5+1 11/15)если не сложно,...
3 - Построите равносторонний треугольник периметр которого равен...
1 - Какое название носила крестьянская община?...
3
(√3)-1
Решение
Сначала мы можем загнать (x+π/6) под знак дифференциала , т. е. dx=d(x+π/6)
Так как d(x+π/6)=dx нечего в интеграле не поменяется , но теперь мы будем интегрировать по переменой x+π/6
x+π/6 мы мысленно можем заменить на t
Тогда получим интеграл от функции dt/sin²t
такой интеграл равен -1/tg(t)
Теперь делаем обратную замену , получаем -1/tg(x+π/6)
tg-тангенс , (если что) .
Потом просто нужно подставить пределы интегрирования , и после сокращения будет (√3)-1
Более подробное решение находится на фотографии выше ↑
Удачи в следующих вычислениях