I. Определить:
1. нормальный вектор прямой a ;
2. угол между прямыми a b ;
3. расстояние от точки A(x y) до прямой b;
4. взаимное расположение прямых a c , в случае их пересечения найти точку пересечения.
Составить:
5. каноническое, нормальное уравнения, уравнение в отрезках и уравнение с угловым коэффициентом
прямой c ;
6. уравнение прямой, проходящей через точку A(x y) параллельно прямой c ;
7. уравнение прямой, проходящей через точку A(x y) перпендикулярно прямой c .
II. Составить канонические уравнения: а) эллипса
б) гиперболы
с) параболы,
если А, В - точки, лежащие на кривой, F – фокус, а – большая (действительная) полуось, b – малая (мнимая полуось), ε - эксцентриситет, y=+-kx - уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние.
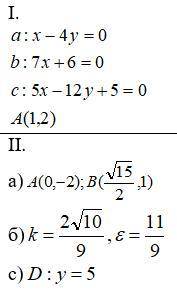
Ответы
Показать ответы (3)
Другие вопросы по теме Математика
Популярные вопросы
- Почему на реке лене нет порогов и водопадов, а на её притоке вилюе...
3 - Текст на казахском языке на тему школьшые каникулы...
1 - Составить 7 предложений на тему мой любимый вид спорта.!...
3 - 97218: 982= 460598: 792= 144560: 695= 1107738: 369= решите в столбиком...
1 - Напишите сочинение по теме является ли изба и баня родственными...
1 - Семья николаевых решила отдохнуть летом за границей.рассчитав свой...
1 - Магазин закупает цветочные горшки по оптовой цене 120 рублей за...
2 - Разделить слово енот на слоги,сколько звуков в первом слоге?...
2 - На 24 рубля купили 8 одинаковых открыток. сколько таких же открыток...
2 - 55 до гипотенузы прямоугольного треугольника проведено высоту и...
3