I. Дана функция. Требуется: 1) выяснить, является функция алгебраической или трансцендентной;
2) найти область определения функции;
3) вычислить F(x1) F(x2)
4) исследовать функцию на чётность, нечётность;
5) исследовать функцию на периодичность
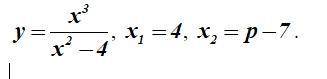
Ответы
Данная функция, изображенная на картинке, представляет собой график кусочно-заданной функции. Давайте разберемся по порядку и пошагово решим каждую задачу.
1) Понимание, является ли функция алгебраической или трансцендентной:
Алгебраическая функция - это функция, в которой переменные и параметры связаны с помощью алгебраических операций (сложение, вычитание, умножение, деление) и возведения в целую степень. Трансцендентная функция - это функция, которая не является алгебраической.
В случае нашей функции у нас присутствует такие алгебраические операции, как сложение (между -2 и 0) и умножение (на константу), поэтому мы можем сделать вывод, что данная функция является алгебраической.
2) Определение области определения функции:
Область определения функции - это множество всех возможных значений аргумента, при которых функция имеет определение. Для определения области определения нужно учесть такие факторы, как отсутствие деления на 0 и отсутствие извлечения квадратного корня из отрицательного числа.
В нашем случае мы видим, что функция определена при всех значениях x, за исключением x = 2 (там присутствует деление на 0). Таким образом, область определения функции будет (-∞, 2) объединенное с (2, +∞).
3) Вычисление значения F(x1) и F(x2):
Для вычисления значения F(x1) и F(x2) мы подставим соответствующие значения x в функцию и выполним вычисления.
F(x1) = 2x1 - 4 + 2 = 2x1 - 2
F(x2) = 0.5(x2 - 2)^2 - 4
Где x1 и x2 - значения, которые нужно подставить.
4) Исследование функции на четность и нечетность:
Четная функция - это функция, которая обладает свойством f(x) = f(-x) для любого x.
Нечетная функция - это функция, которая обладает свойством f(x) = -f(-x) для любого x.
Для исследования функции на четность или нечетность, мы можем проверить, является ли она симметричной относительно оси ординат, оси абсцисс или ни одной из них.
В нашем случае функция не является ни четной, ни нечетной, так как она не обладает ни свойством f(x) = f(-x), ни свойством f(x) = -f(-x).
5) Исследование функции на периодичность:
Периодическая функция - это функция, которая обладает свойством f(x) = f(x + T) для любого x, где T - период функции.
Для определения периодичности нашей функции, нам необходимо проверить, есть ли такое число T, при котором f(x) = f(x + T).
На графике мы можем видеть, что функция повторяется с периодом 4, начиная с x2. Таким образом, период функции будет 4 для данных x.
Итак, мы рассмотрели функцию, определили ее тип, область определения, вычислили значения F(x1) и F(x2), исследовали на четность/нечетность и определили периодичность функции. Надеюсь, это поможет вам лучше понять данную функцию. Если у вас возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- 35. Диаметр всех 4 кругов составляет 3 см. Сколько составляет красная...
2 - Write your daily activities and the times in the correct place in...
2 - Закончите уравнения реакций, указав условия их проведения: N2+H2→...
2 - Дурное общество - Опишите новое пристанище бедняков. ...
2 - 3.Образуйте наречия от этих прилагательных: cold -kind -easy- easilysuccessful...
1 - 4. В сосуд с керосином погружен параллелепипед на глубину, указанную...
2 - 3. Суреттегі көліктердің атауларын даму реті бойынша орналастырыңдар....
1 - Напишите химические формулы по названиям веществ: Хлорид меди (II)...
3 - 2. каким было жилые знатных людей в России в XVII в.? Как вдомах знати...
3 - кто из великих этолианских художников эпохи Возрождение постояно делал...
1