1. Математика
  2. Хелп скоро вступительные,

Хелп скоро вступительные, решить не получается найти абсциссы точек, в которых касательная к графику функции y=x-4/x-2 параллельна прямой y-8x+10=0.

tanuskin798 tanuskin798    1   27.09.2019 06:30    3

Ответы
nikitinallllll nikitinallllll  16.08.2020 23:06

т.к. параллельные прямые имеют одинаковые угловые коэффициенты, по условию k = 8 = f ' (x₀) --это значение производной функции в точке, x₀ это искомая абсцисса точки...

нужно взять производную f ' (x) = y' =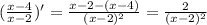 (\frac{x-4}{x-2})'=\frac{x-2-(x-4)}{(x-2)^{2}}=\frac{2}{(x-2)^{2}}

и решить уравнение: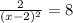 \frac{2}{(x-2)^{2}} =8

(x-2)² = ¹/₄

два решения: или х = 2.5 или х = 1.5

(просто так) уравнение касательной для функции f(x): у = f(x₀) + f ' (x₀) * (x-x₀)

ПОКАЗАТЬ ОТВЕТЫ
карина1543 карина1543  16.08.2020 23:06

Если прямые параллельны, то их угловые коэффициенты "k" равны:

y-8x+10=0 => y=8x-10 => k=8

Находим производную исходной функции:

y=\frac{x-4}{x-2} \\ \\ y'=\frac{x-2-x+4}{(x-2)^2} =\frac{2}{(x-2)^2}

Геометрический смысл производной:

y'(x_0)=k=tg\alpha

В нашем случае достаточно:

y'(x_0)=k \\ \\ \frac{2}{(x_0-2)^2} =8 \\ \\ (x_0-2)^2=\frac{4}{8}=\frac{1}{4} =0.25\\ \\ x_0-2=^+_-\sqrt{0.25} \\ \\ \begin{bmatrix}x_0-2=0.5\\ x_0-2=-0.5 \end{matrix} \Leftrightarrow \begin{bmatrix}x_0=2.5\\ x_0=1.5 \end{matrix} \\ \\ \\ OTBET: \ 1.5; \ 2.5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Angelina1355555 Angelina1355555  03.06.2019 15:40
Разделите 7940 на 40 6780 на 90 47350 на 60 23070 на 40...
yevdokimenkoal yevdokimenkoal  03.06.2019 15:40
Подчеркни синим уравнения с двумя корнями и запиши эти корни. 8*(7-t)=48 r*(r-10)=0 9p-81-9p (x-3)*(5x-20)=0 7d+70=7d+35 (y-8)*3y=0 подчеркни красным уравнения,у которых нет решений...
morginen morginen  03.06.2019 15:40
1. найдите значение выражения: а) раскрыв скобки: 34,4 – (18,1 – 5,6) + (-11,9 +8)б) применив распределительное свойство умножения: 2. выражение: а) 4m – 6m – 3m+7+mб) -8(к-3)+4(к-2)-2(3к+1)в)...
DashaLatysheva1 DashaLatysheva1  03.06.2019 15:40
Зная ,что с 1 марта в каждую из трех аптек города каждую неделю привозят 4500 упаковок новых витаминов,ответь на следующие вопросы: 1. каждую неделю аптека№1 продает 3750 упаковок...
meskov meskov  03.06.2019 15:40
Водной фляге было 24 кг сметаны а в другой 36 кг из первой фляги взяли восьмую. часть сметаны а из второй девятую часть сколько килограммов сметаны взяли из двух фляг? сколько сметаны...
vanuaevstifeev vanuaevstifeev  03.06.2019 15:40
Высота окна 156 см,а ширина составляет 2/3 от высоты.сколько см.кв.составит площадь окна...
sasha200121 sasha200121  03.06.2019 15:40
На пакете с мукой надпись 1.5 кг. 105 тг . какова цена 1 кг. муки? !...
Elizaveta30122005 Elizaveta30122005  03.06.2019 15:40
Два пешехода вышли одновременно из одного места в противоположных направлениях. через 0,8 часов расстояние между ними стало равным 6,8 км. скорость одного пешехода была в 1,5 раза...
Оля2204202 Оля2204202  03.06.2019 15:40
Решите . 1.в первый день рабочий перевыполнил дневное на 2%,во второй день он перевыполнил на 4%.на сколько процентов рабочий перевыполнил двух дней? 2.в спортивной секции девочки...
Viktoria818 Viktoria818  03.06.2019 15:40
Напишите все целые значения z , если 5 |z| 9 ....

Популярные вопросы