Haйти площадь фигуры D ограниченной линиями:
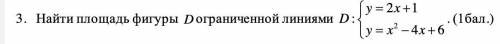
Другие вопросы по теме Математика
Популярные вопросы
- Выпиши из предложение 4 местоимения,укажи лицо и число. текст: звали его...
1 - Сдетства родители1 и мальчишки с девчонками удивлялись на аркашу3 пластова4....
2 - 1)для функции f(x)=5x^4-2 найдите первообразную,график которой проходит...
2 - Вкакой горной породе или полезном ископаемом можно увидеть остатки морских...
2 - Определить количество вещества гидроксида калия в 1000г...
1 - Как исправить : подъезжая к станции и глядя на вокзал в окно, меня охватила...
2 - Яка дія струму закладeна в дію eлeктровимірювальних приладів...
3 - Поезд отошёл от станции с ускорением 0,5м/с^2. за какое время он достигнет...
2 - 2. 1. найдите предложение, в котором выделенное слово представляет собой...
1 - Верно ли утверждение? при животных к условиям среды выражена только во...
3
Пошаговое объяснение: