Характеристические многочлены вещественных матриц размера 2\times 22×2 AA и BB совпадают. Но нет оператора, что в каком-то базисе он записывается матрицей AA, а в каком-то --- матрицей BB. След матрицы AA равен 10. А чему равен определитель матрицы BB?

$Характеристические многочлены вещественных матриц размера 2\times 22×2 AA и BB совпадают. Но нет опе$

Ответы

vipsab333 21.06.2021 13:29

По условию характеристические многочлены матриц второго порядка А и В совпадают. Поскольку характеристический многочлен ищется по формуле

$\lambda^2- Tr\ a\cdot \lambda+\det A =0,$ делаем вывод, что

$Tr\ A =Tr\ B;\ \det A=\det B.$

Если бы корни характеристического уравнения были бы разные, все матрицы с таким характеристическим уравнением были бы подобны, то есть были бы матрицами одного и того же оператора. Но по условию это не так. Вывод: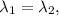 $\lambda_1=\lambda_2,$ а матрицы второго порядка с таким условием бывают двух видов: - скалярная матрица (а поскольку по условию след равен 10, это скалярная матрица 5E, где E - единичная матрица), и те, которые подобны жордановой клетке с пятерками на диагонали. Поскольку определитель матрицы (как и ее след) не зависят от выбора базиса, делаем вывод, что определители матриц А и В равны 25.

ответ: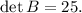 $\det B = 25.$

Замечание. Зачем было путать потенциальных "решателей" и писать в условии AA и BB вместо А и В? Не понимаю.

Замечание. Tr A - это обозначение для следа матрицы, то есть суммы элементов, стоящих на главной диагонали, det A - обозначение для определителя матрицы.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика