х(в степени n-2)*x(в степени 3-n)*x
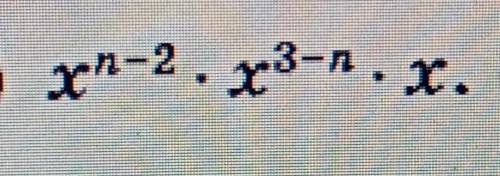
Другие вопросы по теме Математика
Популярные вопросы
- Лишь суслики во ржи скликаются свистками, иль по меже тушкан, таинственно,...
1 - 3. use the verb must as in the model and translate the sentences. example:...
3 - Найдите значение выражения – 8 + (– 5) – 3 ∙ (– 4)....
1 - Розібрати прислівники за будовою(тихо,швидко)...
1 - Предпосылки возникновения казачества?...
2 - Вполях созрел ячмень он радует меня! брожу я целый день по волнам ячменя...
3 - C- co- co2- h2co3 и fe- feo- fe2o3- fe(oh)3...
3 - 1.перечисли три жанра сюжетной композиции? назови хотя бы одну картину...
1 - 3х+2у=20 решите это уравнение за ранее ....
2 - Напишите сочинение по впечатлениям, от прочитанного рассказа белогрудка...
3
...............................................
Правило умножения: a * b * c = a * (b * c)
Правило возведения в степень: (a^b) * (a^c) = a^(b+c)
В данной задаче у нас есть произведение трех множителей: х^(n-2), х^(3-n) и х. Мы можем применить правило умножения и записать произведение в следующем виде:
x^(n-2) * x^(3-n) * x.
По правилу возведения в степень, мы можем сложить степени с одинаковыми основаниями. В данном случае, у нас есть основание x, поэтому степени n-2 и 3-n могут быть сложены:
x^(n-2) * x^(3-n) * x = x^[(n-2) + (3-n)] * x.
Мы можем упростить выражение внутри квадратных скобок, произведя сложение:
x^(n-2) * x^(3-n) * x = x^(n-2+3-n) * x.
Теперь мы получили выражение x^1, заметьте, что степень равна 1. Значение x в любой степени, равной 1, всегда будет равно самому x. Следовательно, ответ на данный вопрос равен x.
Итак, ответ на данный вопрос: x.