Градиент функции z=2x^2-3xy+y^3 в точке M0 (2;1) равен…
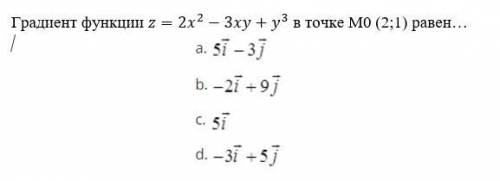
Другие вопросы по теме Математика
Популярные вопросы
- Композиція твору Золотой Жук...
2 - Вкладки с полным сопротивлением проводника 25 Ом и сопротивлением...
1 - Объясните кто такие головохоботные черви и кто к ним относится. Относятся...
3 - Выполните с действия номер...
2 - Сравнительная таблица Франции и Англии 17 в. на тему: характеристика...
1 - ответьте на во сірочы хлеб) Хто такі Мікола Кужалевіч?...
1 - ответьте на во сірочы хлеб) Якую кнігу пані Мар я падарыла Даніку?...
3 - Запишите уравнения второго закона Ньютона для движения тела со скоростью...
1 - Яка протока відокремлює Мадагаскар від Африки? До ть...
3 - Чаму Янка Брыль назваў сваю аповесць сірочы хлеб ?...
3
По определению, частная производная по переменной x означает, что мы считаем все переменные, кроме x, постоянными и дифференцируем функцию только по x. Аналогично, частная производная по переменной y означает, что мы считаем все переменные, кроме y, постоянными и дифференцируем функцию только по y.
Итак, вычислим частные производные:
Частная производная по x:
∂z/∂x = d(2x^2)/dx - d(3xy)/dx + d(y^3)/dx
= 4x - 3y
Частная производная по y:
∂z/∂y = d(2x^2)/dy - d(3xy)/dy + d(y^3)/dy
= 0 - 3x + 3y^2
= -3x + 3y^2
Теперь, чтобы найти градиент в точке M0, мы подставим значения x=2 и y=1 в найденные частные производные:
∂z/∂x (M0) = 4*2 - 3*1 = 8 - 3 = 5
∂z/∂y (M0) = -3*2 + 3*1^2 = -6 + 3 = -3
Таким образом, градиент функции z=2x^2-3xy+y^3 в точке M0 (2;1) равен вектору (5, -3).
Обоснование: Градиент функции представляет собой вектор, указывающий направление наибольшего роста функции в данной точке. Вектор градиента также перпендикулярен поверхности уровня функции в точке M0 и указывает направление наискорейшего роста функции. Таким образом, вектор (5, -3) указывает направление наибольшего роста функции z=2x^2-3xy+y^3 в точке M0 (2;1).