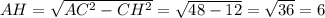Гипотенуза прямоугольного треугольника равна 8, а один из катетов 4. найти длину проекции другого катета на гипотенузу.
Другие вопросы по теме Математика
Популярные вопросы
- Оксид фосфора(V) реагирует с веществами:NaOHNa2 SО4Н2SO4Li2O...
3 - 6.В каком слове есть только твёрдые согласные звуки: А) мел В) можешь С) ярмо D)...
3 - Напишите предложение в сказке были Кладовая солнца 30-40 слов...
2 - Что защищает землю от вредного солнечного влияния литосфера стратосфера атмосфера...
2 - Укажите тип реакцииAgNO3 + HCl =Na2SO4 + BaCl2 =CuCl2 + NaOH=Na2S + HCl =...
3 - Какие из указанных на рисунке поверхностей зеркальные? 1) 1 и 3 2) 2 и 4 3) 3 и...
2 - На рисунке приведен график движения пешехода в течение трех часов. Чему равна средняя...
2 - Длина садового питомника — 729 дм, его периметр — 1926 дм. Чему равна площадь садового...
3 - До якої частини мови належать слова весело сьогодні зверху навесні...
2 - 2) Закончить уравнение реакции, расставить коэффициенты, назвать продукты реакции...
1
АВС - труегуольник, угол С - прямой, AB=8, BC=4. Проведем высоту СН к гипотенузе AB. АН - проеция катета АС на гипотенузу АВ.
По т.Пифагора
Высота, опущенная на гипотенузу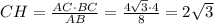
Тогда из тр-ка ACH