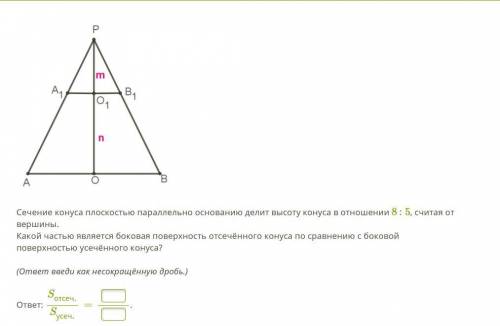
ГЕОМЕТРИЯ Сечение конуса плоскостью параллельно основанию делит высоту конуса в отношении 8 : 5, считая от вершины.
Какой частью является боковая поверхность отсечённого конуса по сравнению с боковой поверхностью усечённого конуса?

Для решения этой задачи, нам нужно сначала понять, какое отношение сечение конуса делит высоту. Затем мы можем вычислить отношение площадей боковых поверхностей отсеченного и усеченного конусов.

В данной задаче сечение делит высоту конуса в отношении 8 : 5, считая от вершины. Это значит, что расстояние от вершины конуса до сечения делится на две части: одна равна 8, а другая равна 5. Мы можем обозначить эти расстояния как h1 и h2.

Теперь давайте рассмотрим боковую поверхность отсеченного конуса. Она состоит из двух частей: основного конуса и отсечения. Давайте обозначим площади этих частей как S1 и S2.

Площадь боковой поверхности основного конуса можно вычислить с использованием формулы S1 = πrl, где r - радиус основания конуса, l - образующая конуса. Мы можем найти r и l по информации, данной в задаче. В задаче не указан радиус конуса, но мы можем найти его, используя теорему Пифагора в треугольнике, образованном радиусом, образующей и высотой конуса:

r^2 + h^2 = l^2

Заметим, что в отсеченном конусе высота равна (h1 - h2), а образующая остается такой же.

Поэтому площадь боковой поверхности основного конуса S1 = πr1l1

Для вычисления площади отсечения S2, мы должны знать радиус основания отсеченного конуса r2 и высоту отсечения h1-h2. Мы можем использовать аналогичную формулу S2 = πr2l2.

Далее, нам нужно найти отношение площадей S2 к S1. Это делается путем деления S2 на S1.

Таким образом, для того чтобы выразить отношение боковых поверхностей отсеченного и усеченного конусов, необходимо провести следующие шаги:

1. Найти радиус основания большего конуса r1 и его образующую l1 с использованием теоремы Пифагора.

2. Найти радиус основания отсеченного конуса r2 и его образующую l2, зная высоту отсечения (h1 - h2).

3. Вычислить площадь боковой поверхности основного конуса S1 = πr1l1.

4. Вычислить площадь боковой поверхности отсечения S2 = πr2l2.

5. Выразить отношение боковых поверхностей отсеченного и усеченного конусов: S2/S1.

Следуя этим шагам, мы получим ответ на задачу и сможем объяснить его школьнику с максимальной ясностью и подробностью.